A point particle of mass m, moves long the uniformly rough track PQR as shown in figure. The coefficient of friction, between the particle and the rough track equals μ. The particle is released, from rest from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR.
The value of the coefficient of friction μ and the distance x (=QR), are, respectively close to:

0.2 and 3.5m
0.29 and 3.5m
0.29 and 6.5m
0.2 and 6.5m
The correct Answer is:B
Energy lost over path PQ
=μmgcos30∘×4........(i)
Energy lost over path QR
=μmgx...........(ii)
By (i) and (ii)
μmgx=μmgcos30∘×4
⇒x=4×√32=2√3=3.45m≈3.5m

Since , From Q to R energy lost is half of the total energy
μmgx=12mgh⇒μ=0.29.
Aliter : Given, μmghtanθ=mgh−μmghtanθ
2μtanθ=1⇒μ=tanθ2=tan30∘2⇒μ=0.29
x=htanθ=2√3≈3.5m
Similar Questions
m ভরের একটি কণা একটি অমসৃণ পথ PQR বরাবর চলছে পথ এবং কণাটির মধ্যে ঘর্ষণ গুণাঙ্ক μ। P বিন্দু থেকে কণাটিকে ছেড়ে দেওয়া হল এবং সেটি R বিন্দুতে পৌঁছে স্থির অবস্থায় এল। কনাটি তার যাত্রাপথের PQ এবং QR অংশ যেতে সমপরিমাণ শক্তি হারায়। এক্ষেত্রে কণাটি PQ পথ থেকে অভিমুখ পরিবর্তন করে QR পথে যেতে কোন শক্তি ক্ষয় না হলে ঘর্ষণ গুণাঙ্ক ও QR পথের দৈর্ঘ্য (x)যথাক্রমে-
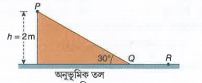
View SolutionA point particle of mass m, moves long the uniformly rough track PQR as shown in figure. The coefficient of friction, between the particle and the rough track equals μ. The particle is released, from rest from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR.
The value of the coefficient of friction μ and the distance x (=QR), are, respectively close to:

View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View Solutionm' द्रव्यमान का एक बिंदु कण एक खुरदरे पथ PQR (चित्र देखिये) पर चल रहा है । कण ओर पथ के बीच घर्षण गुणांक μ है । कण P से छोड़े जाने के बाद R पर पहुंच कर रुक जाता है। पथ के भाग PQ ओर QR पर चलने में कण द्वारा खर्च की गई ऊजायें बराबर है । PQ से QR पर होने वाले दिशा बदलाव में कोई ऊर्जा खर्च नहीं होती । तब μ ओर दुरी x(= QR) के मान लगभग है क्रमश:
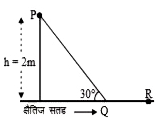
View SolutionA point particle of mass m, moves long the uniformly rough track PQR as shown in figure. The coefficient of friction, between the particle and the rough track equals mu . The particle is released, from rest from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR. The value of the coefficient of friction mu and the distance x (=QR) , are, respectively close to:
View SolutionA block weighing 10 N travels down a smooth curved track AB joined to a rough horizontal surface (figure). The rough surface has a friction coefficient of 0.20 with the block. If the block is released from rest on the track from a point 1.0 m above the horizontal surface, the distance it will move on the rough surface is

View SolutionA particle of mass m=5.00kg is released from point A and it slides on the frictionless track shown in figure. Determine (a) the particle's speed at points B and C and (b) the net work done by the gravitational force as the particle moves from A to C.
View SolutionFigure shows a circular frications trck of radius R, centred at point O. A particle of mass M is released from point A(OA=R/2). After collision with the track, the particle moves along on the track. Then the coefficient of restitution e is.

View Solution