Figure shows a circular frications trck of radius R, centred at point O. A particle of mass M is released from point A(OA=R/2). After collision with the track, the particle moves along on the track. Then the coefficient of restitution e is.

0.2
0.5
1
zero
The correct Answer is:D
cosθ=12⇒θ=π3
(a) After collision the particle moves along the track. This means there is no normal component of velocity, Hence e=0
(b) Just before collision, the compoenents of velocity along the normal and along the tangent are
un=usinθ
ut=ucosθ

During collision ut does not change. The normal component of velocity becomes eun along →BO.
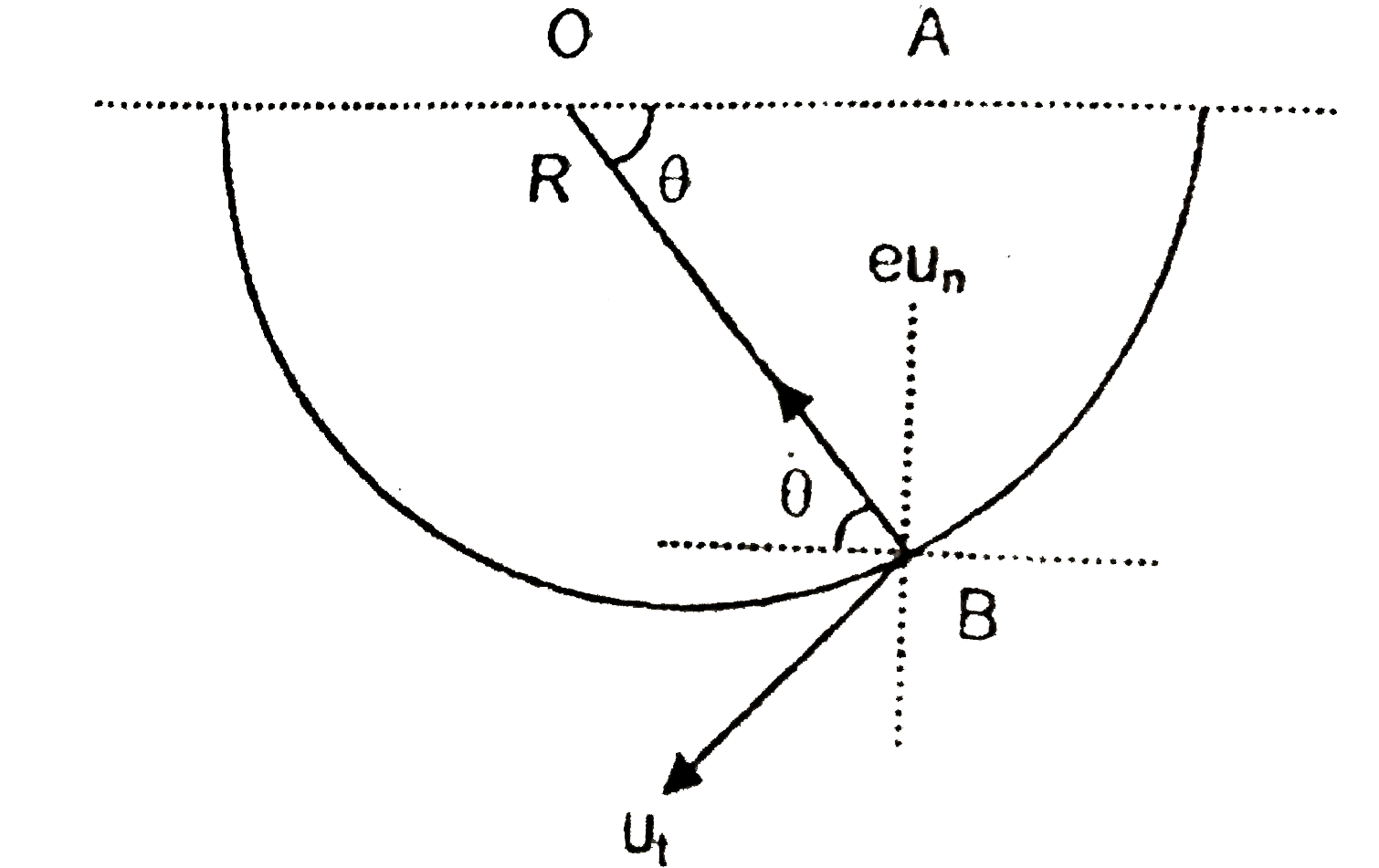
Question says that velocity of the particle is horizontal after collision, which mean sutcosθ=eunsinθ
ucos2θ=eusin2θ⇒e=cot2'π3=13
Similar Questions
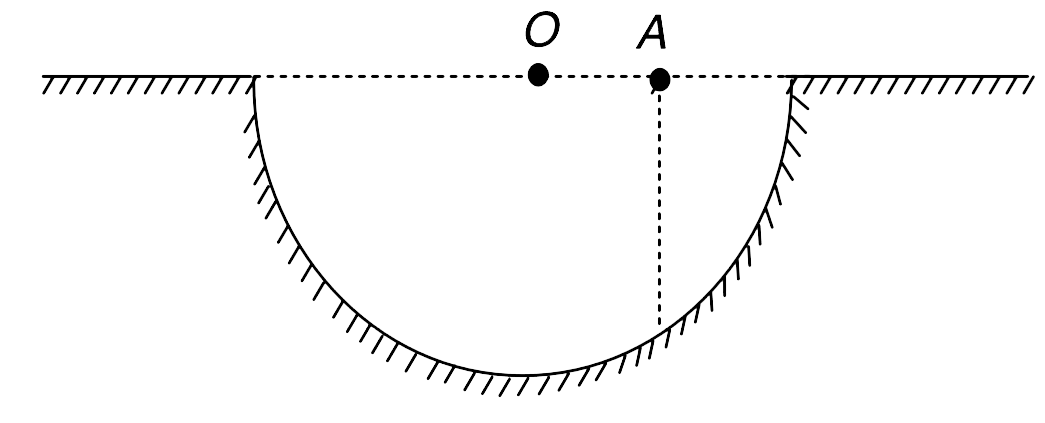
Figure shows a circular frictionless track of radius R, centred at point O. A particle of mass M is released from point A(OA=R/2). After collision with the track, the particle moves along the track.
(a) Find the coefficient of restitution e.
(b) What will be value of e if the velocity of the particle becomes horizontal just after collision ?
View SolutionA circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
View Solution
Knowledge Check
A particle of mass m, collides with another stationary particle of mass M. If the particle m stops just after collision, then the coefficient of restitution for collision is equal to
A1BmMCM−mM+mDmM+mA particle of mass m is suspended from point O and undergoes circular motion in horizontal plane as conical pendulum as shown in figure.
 AAngular momentum of particle about point of suspension does not remains constant.BAngular momentum of particle about centre of circle remains constant.CAverage force during half rotation is 2mgtanthethaπDAverage torque about axis OC during half rotation is zero
AAngular momentum of particle about point of suspension does not remains constant.BAngular momentum of particle about centre of circle remains constant.CAverage force during half rotation is 2mgtanthethaπDAverage torque about axis OC during half rotation is zero
A particle of mass m is released from point A as shown in the gigure. Would it loop the loop if H=4r? What is the force on the circular track when it is at point (a) B, (b) C?

View SolutionFigure shows a particle slideing on a frictionles track which terminates in straight horizontal section. If the particle starts slipping from the point. A, how far way from the track will the particle hit the ground ?
View SolutionA block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A. Find the velocity of sphere and track , when the sphere reaches B.

View SolutionShown a smooth looping the loop track A particle of mass m is released from oint A , as shown If H = 3 r , whould the particle loop the loop ? What is the force on the circular track when the particle is at point (i) B (ii) C ? .
View SolutionA smooth wedge of mass M is kept at rest on a smooth horizontal surface . Inclined face of the wedge make an angle θ with the horizontal . A particle of mass m collides normal to inclined face of wedge . If speed of the particle just before collision is u and coefficient of restitution is e then find velocity of wedge after collision .
View SolutionA particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?
View Solution