The position of a particle moving on a straight line is proportional to the cube of the time elapsed. How does the acceleration of the particle depend on time elapsed?
a∝t2
a∝2t
a∝t3
a∝6t
The correct Answer is:D
x∝t3
v=dxdt∝3t2
a=dvdt∝6t
Similar Questions
A particle at rest is moved along a straight line by a machine giving constant power. The distance moved by the particle in time 't' is proportional to
View SolutionThe displacement of a body is given to be proportional to the cube of time elapsed. The magnitude of the acceleration of the body is
View SolutionThe velocity of a particle moving in a straight line is directly proportional to 3//4th power of time elapsed. How does its displacement and acceleration depend on time?
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
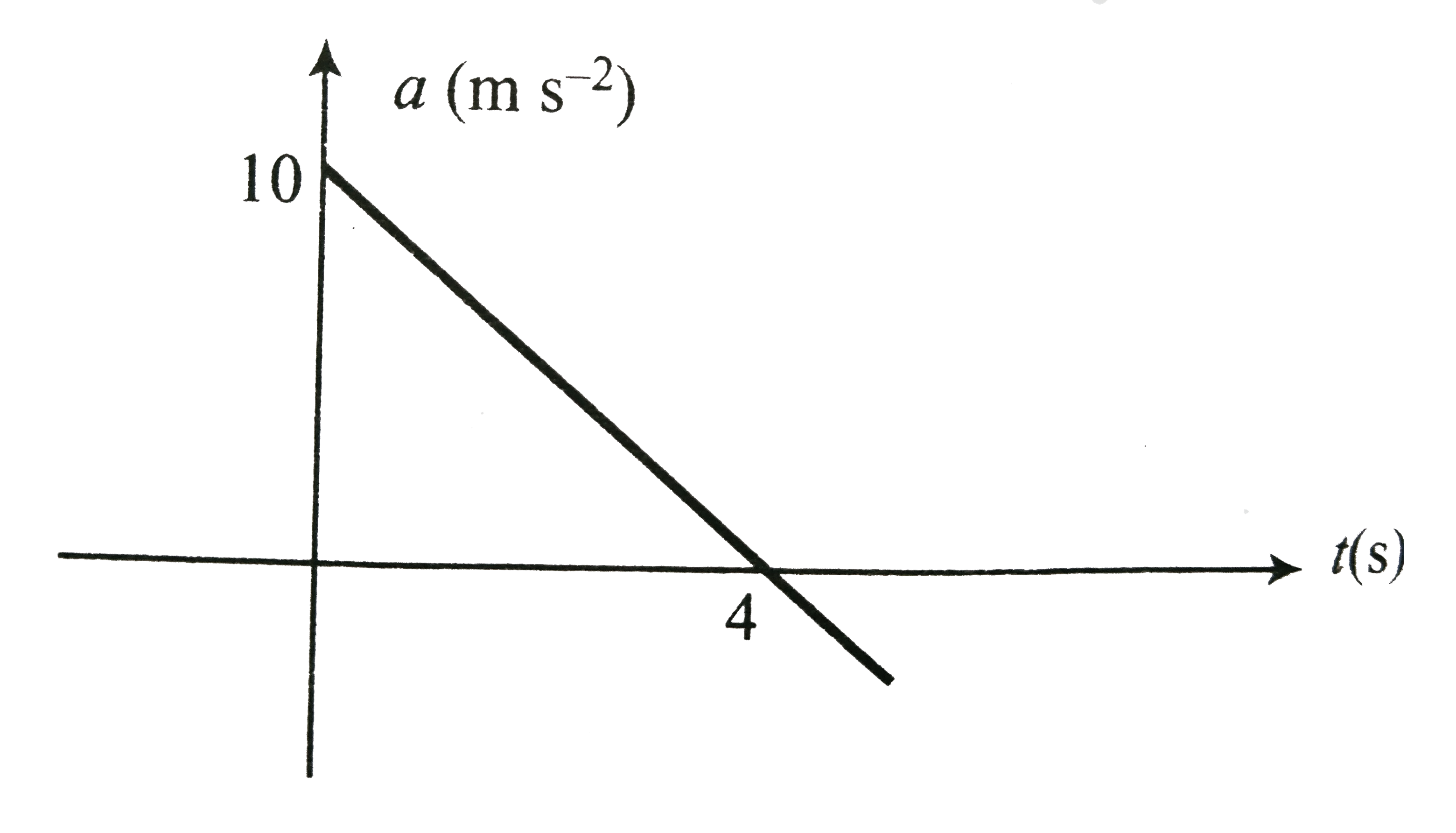 .
.
View SolutionThe acceleration versus time graph of a particle moving in a straight line is show in. The velocity-time graph of the particle would be
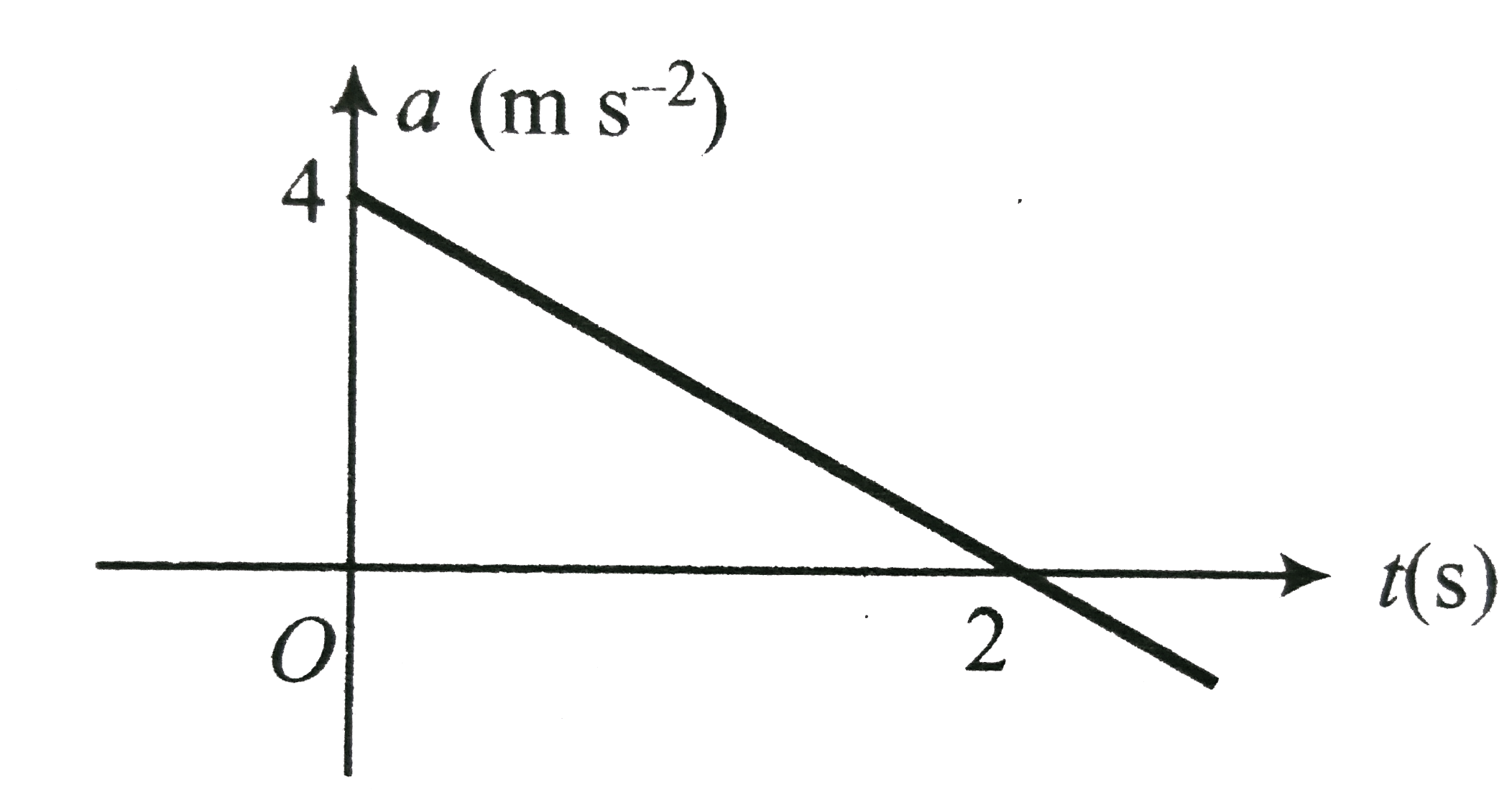 .
.
View SolutionThe position of a particle moving on a straight line is proportional to the cube of the time elapsed. How does the acceleration of the particle depend on time elapsed?
View SolutionThe distance travelled by a particle in a straight line motion is directly proportional to t^(1//2) , where t is the time elapsed.
View SolutionA particle starts from rest and covers a distance on a straight path in direct proportion to the square of time elapsed. What can one conclude about its acceleration?
View Solution