The position of a particle moving on a straight line is proportional to the cube of the time elapsed. How does the acceleration of the particle depend on time elapsed?
Video Solution
Text Solution
Let x be the position at time instant t of the particle in motion. Given x=kt3, where k is a constant of proportionality. The velocity of particle can be calculated as v=dxdt=3kt2 and acceleration of object can be calculated as
a=dvdt=ddt{3kt2]=3kddt(t2)
a=3k(2t2−1)=6kt
i.e., a∝t. It means acceleration ∝ time.
|
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Try Yourself
Explore 40 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - A)
Explore 50 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
- MOVING CHARGE AND MAGNESIUMBook:AAKASH INSTITUTEChapter:MOVING CHARGE AND MAGNESIUMExercise:SECTION D
Explore 16 Videos
Similar Questions
Knowledge Check
Kinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
ADirectly proportional to the speed of the particleBInversely proportional to √tCInversely proportional to the speed of the particleDDirectly proportional to √tThe position of a particle moving on a straight line depends on time t as
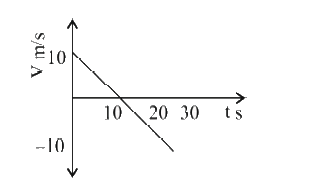
x=(t+3)sin(2t)AIts velocity at the initial moment is 6 m/sBIts acceleration at the initial is −8m/s2CIt has velocity of 3 m/s at t=π2 secDIt has an acceleration of 2m/s2 at t=π4 secThe velocity time plot for a particle moving on straight line is shown in the figure.
 AThe particle has a constant accelerationBThe particle has nevedr turned aroundCThe paeticle has zero displacement.DThe average speed in the interval 0 to 10 s is the same as the average speed in the interval 10 s to 20s.
AThe particle has a constant accelerationBThe particle has nevedr turned aroundCThe paeticle has zero displacement.DThe average speed in the interval 0 to 10 s is the same as the average speed in the interval 10 s to 20s.
The velocity- time plot for a particle moving on a straight line is shown in the figure
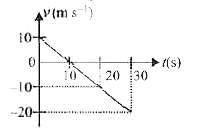
View SolutionThe velocity-time plot for a particle moving on a straight line is shown in figure.
View SolutionThe displacement of a particle is proportional to the cube of time. Then magnitude of its acceleration
View SolutionIf average velocity of particle moving on a straight line is zero in a time interval, then
View SolutionThe displacement of a body is given to be proportional to the cube of time elapsed. The magnitude of the acceleration of the body is
View Solution