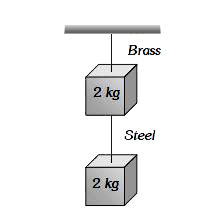
If the ratio of lengths, radii and Young's modulus of steel and brass wires shown in the figure are a, b and c, respectively. The ratio between the increase in lengths of brass and steel wires would be
b2a2c
bc2a2
ba22c
a2b2c
The correct Answer is:D
l1l2=a,r1r2=bandY1Y2=c
Δl1Δl2=F1l1A1Y1×A2Y2F2l2
=2g×l1πr21×Y1×πr22×Y24g×l2
⇒Δl1Δl2=a2b2c
Similar Questions
The Young's Modulus of steel is twice that of brass. Two wires of same length and of same area of cross-section, one of steel and another of brass are suspended from the same roof. If then the weights added to the steel and brass wires must be in the ratio of
View SolutionThe ratios of length areas of cross-section and Young's modulii of steel of that of brass wires shown in the figure are a,b and c respectively . The ratio of increase in the lengths of brass of that of steel wires is [Assume that the masses of steel and brass wires are negligible]
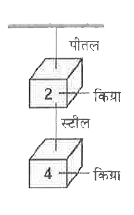
View Solutionचित्र में दिखाए गए स्टील तथा पीतल के तारों की लम्बाइयों, त्रिज्याओं तथा यंग प्रत्यास्थता गुणांकों में अनुपात क्रमशः a,b तथा c हैं। पीतल के तार की लम्बाई में वृद्धि तथा स्टील के तार की लम्बाई में वृद्धि में अनुपात होगा
View SolutionIf the ratio of lengths, radii and Young.s modulus of the steel and brass rods in the figure are a, b,c respectively, find the ratio of increase in their lengths ?
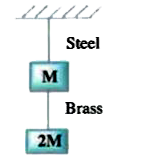
View SolutionIf the ratio of diameters,lengths and Young's moduli of steel and brass wires shown in the figure are p, q and r respectively . Then the corresponding ratio of increase in their lenghts would be
View SolutionIf the ratio of diameter, lengths and Young's modulus of steel and brass wires shown in figure are 2 : 1, 2 : 1 and 2 : 1 respectively, then the corresponding ratio of increase in their lengths would be

View SolutionIf the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a, b and c respectively then the corresponding ratio of increase in their lengths is
View SolutionIf the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a,b and c respectively then the corresponding ratio of increase in their lengths is
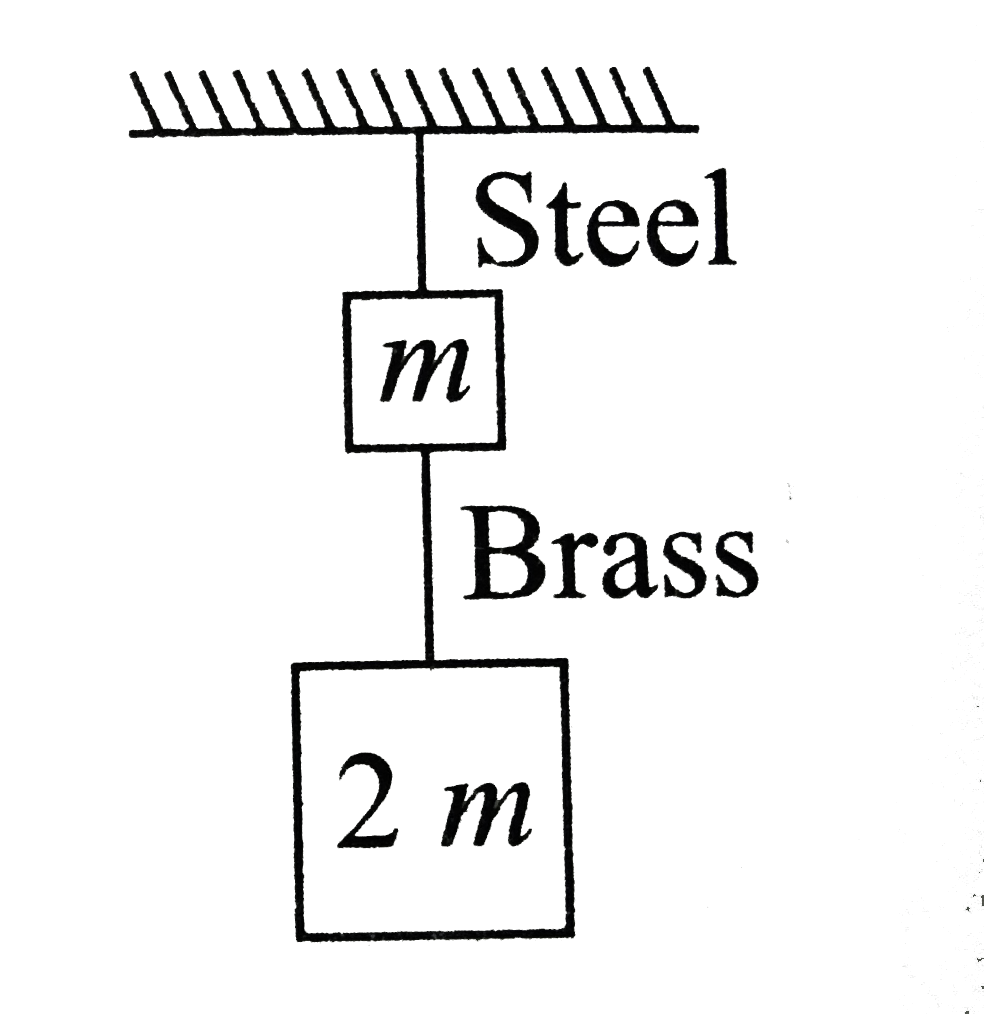
View Solution
