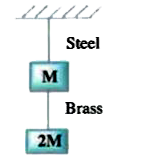
If the ratio of lengths, radii and Young's modulus of steel and brass wires shown in the figure are a, b and c respectively, the ratio between the increase in lengths of brass and steel wires would be Brass and steel wire would be
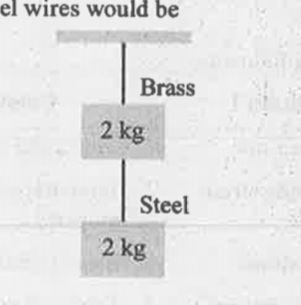 Solution in Telugu
Solution in Telugu
b2ac2c
bc2a2
ba22c
ab2c
The correct Answer is:D
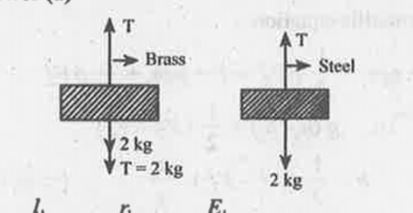
l1l2=a,r1r2=b,E1E2=c
E1=F1A1.lΔl
E2=F2A2.L2Δl2
E1E2=F1A2.l1Δl2F2A1.l2Δl1
Force acting on the steel wire
T=F1=2kg
Forces acting on the brass wire
F2=T2=T+2kg=4kg
∴E1E2=24.π22π21.l1l2.Δl2Δl1
∴C=121b2.aΔl2Δl1
∴Δl1Δl2=a2b2c
Topper's Solved these Questions
Similar Questions
A circular loop and a square loop are formed from two wires of same length and cross section. Same current is passed through them. Then the ratio of their dipole moments is
View SolutionThe dimensions of a/b in the equation p=a−t2bx where P is pressure, x is distance ant 't' is time are,
View SolutionYoung's modulus of brass and steel are 10×1010N/m and 2×1011N/m2, respectively. A brass wire and a steel wire of the same length are extended by 1mm under the same force. The radii of the brass and steel wires are RB and RS. respectively. Then
View SolutionIf the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a, b and c respectively then the corresponding ratio of increase in their lengths is
View SolutionIf the ratio of lengths, radii and youngs's modulus of steel and and brass wires in figure are 2:1,2:1,3:1 respectively. Then corresponding ratio of increases in their would be. (Neglect the mass of the wire and take g=10m/s2)
View SolutionIf the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a,b and c repectively then the corresponding ratio of increase in their lengths is
View SolutionIf the ratio of diameters,lengths and Young's moduli of steel and brass wires shown in the figure are p, q and r respectively . Then the corresponding ratio of increase in their lenghts would be

View SolutionIf the ratio of lengths, radii and young's modulii of steel and brass wires in the figure are a,b and c, respectively. Then, the corresponding ratio of increase in their lengths would be
View SolutionThe Young's modulus of brass and steel are respectively 1.0×1011N/m2 and 2.0×1011N/m2 . A brass wire and steel wire of the same length are extended by 1mm each under the same force. If radii of brass and steel wires are RB and RS respectively,. then
View SolutionThe Young's Modulus of steel is twice that of brass. Two wires of same length and of same area of cross-section, one of steel and another of brass are suspended from the same roof. If then the weights added to the steel and brass wires must be in the ratio of
View SolutionThe ratios of length areas of cross-section and Young's modulii of steel of that of brass wires shown in the figure are a,b and c respectively . The ratio of increase in the lengths of brass of that of steel wires is [Assume that the masses of steel and brass wires are negligible]
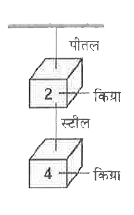
View Solutionचित्र में दिखाए गए स्टील तथा पीतल के तारों की लम्बाइयों, त्रिज्याओं तथा यंग प्रत्यास्थता गुणांकों में अनुपात क्रमशः a,b तथा c हैं। पीतल के तार की लम्बाई में वृद्धि तथा स्टील के तार की लम्बाई में वृद्धि में अनुपात होगा
View SolutionThe Young's modulus of brass and steel are 10 ^(11) Nm ^(-2) and 2 xx 10 ^(11) Nm ^(-2) respectively. A brass wire and a steel wire of the same length extend by 1 mm, each under the same force. If radii of brass and steel wires are R_(B) and R_(S) respectively, then .. .
View SolutionIf the ratio of lengths, radii and Young.s modulus of the steel and brass rods in the figure are a, b,c respectively, find the ratio of increase in their lengths ?
View SolutionIf the ratio of diameters,lengths and Young's moduli of steel and brass wires shown in the figure are p, q and r respectively . Then the corresponding ratio of increase in their lenghts would be
View Solution
