If the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a,b and c repectively then the corresponding ratio of increase in their lengths is
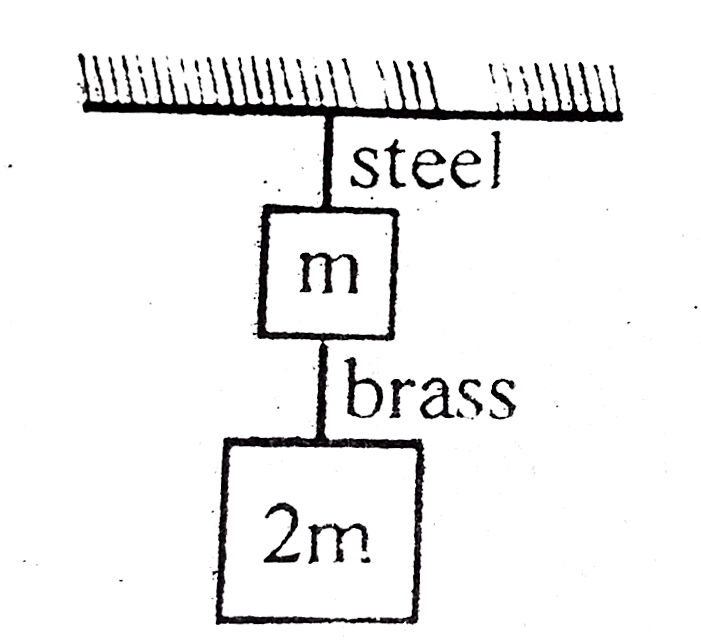
2a2c/b
3a/2b2c
2ac/b2
3c/2ab2
The correct Answer is:B
TS=3mg
3mgAs=yS×ΔlSlS
2mgAb=yb×Δlblb
ΔlsΔlb=32×lslb×AbAS×ybyS=32×ab2c
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Comphrehension
134 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
If the ratio of lengths, radii and young's modulii of steel and brass wires in the figure are a,b and c, respectively. Then, the corresponding ratio of increase in their lengths would be

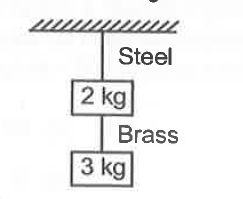
View SolutionIf the ratio of diameter, lengths and Young's modulus of steel and brass wires shown in figure are 2 : 1, 2 : 1 and 2 : 1 respectively, then the corresponding ratio of increase in their lengths would be
View Solution
Knowledge Check
If the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a,b and c respectively then the corresponding ratio of increase in their lengths is
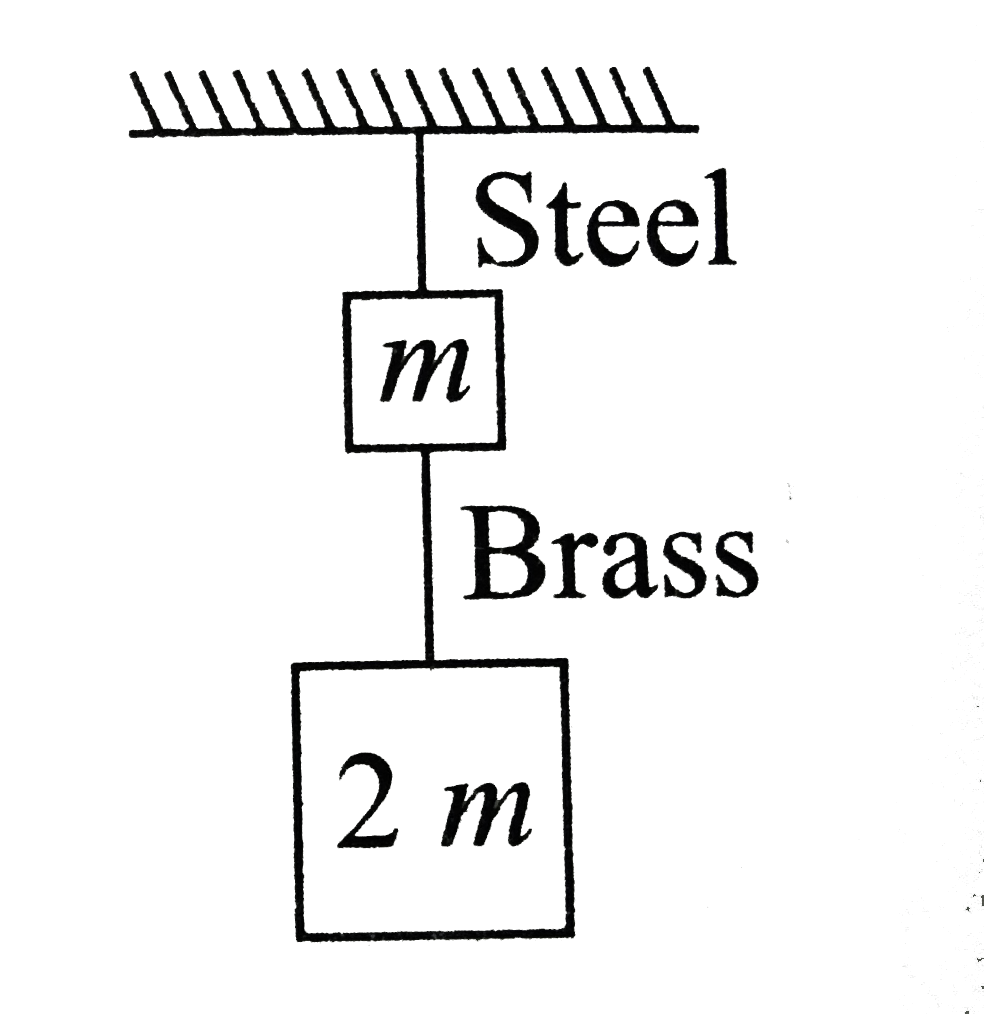 A2a2cbB3a2b2cC2acb2D3c2ab2
A2a2cbB3a2b2cC2acb2D3c2ab2If the ratio of diameters,lengths and Young's moduli of steel and brass wires shown in the figure are p, q and r respectively . Then the corresponding ratio of increase in their lenghts would be
 A3q5p2rB5q3p2rC3q5prD5q3pr
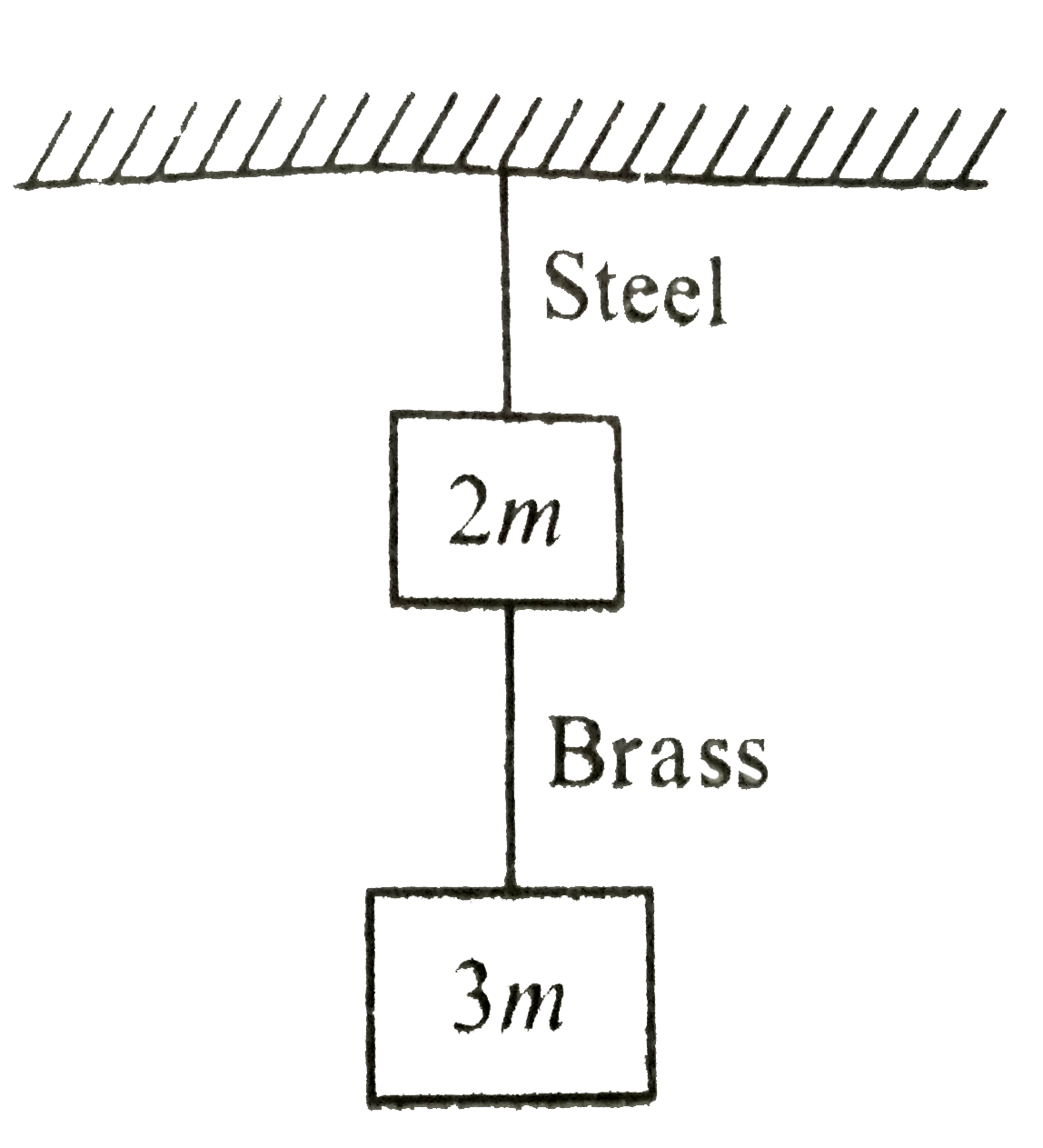
A3q5p2rB5q3p2rC3q5prD5q3prIf the ratio of lengths, radii and youngs's modulus of steel and and brass wires in figure are 2:1,2:1,3:1 respectively. Then corresponding ratio of increases in their would be. (Neglect the mass of the wire and take g=10m/s2)
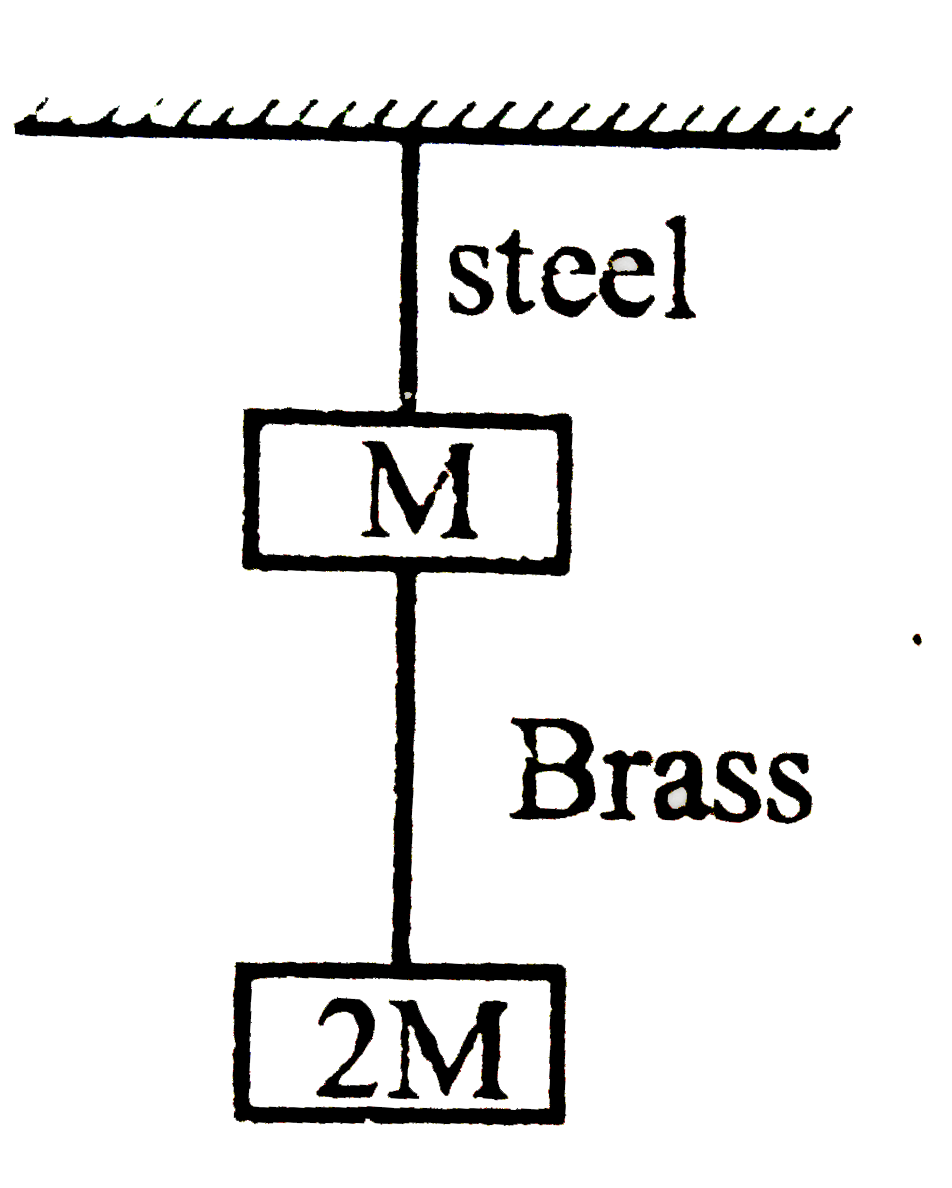 A1:4B8:1C1:3D2:4
A1:4B8:1C1:3D2:4
If the ratio of lenghts, radi and Young's moduli of steel and brass wires are a,b and c respectively their respective loads are in the ratio 3:2 then the corresponding ratio of increases in their lenghts would be
View Solution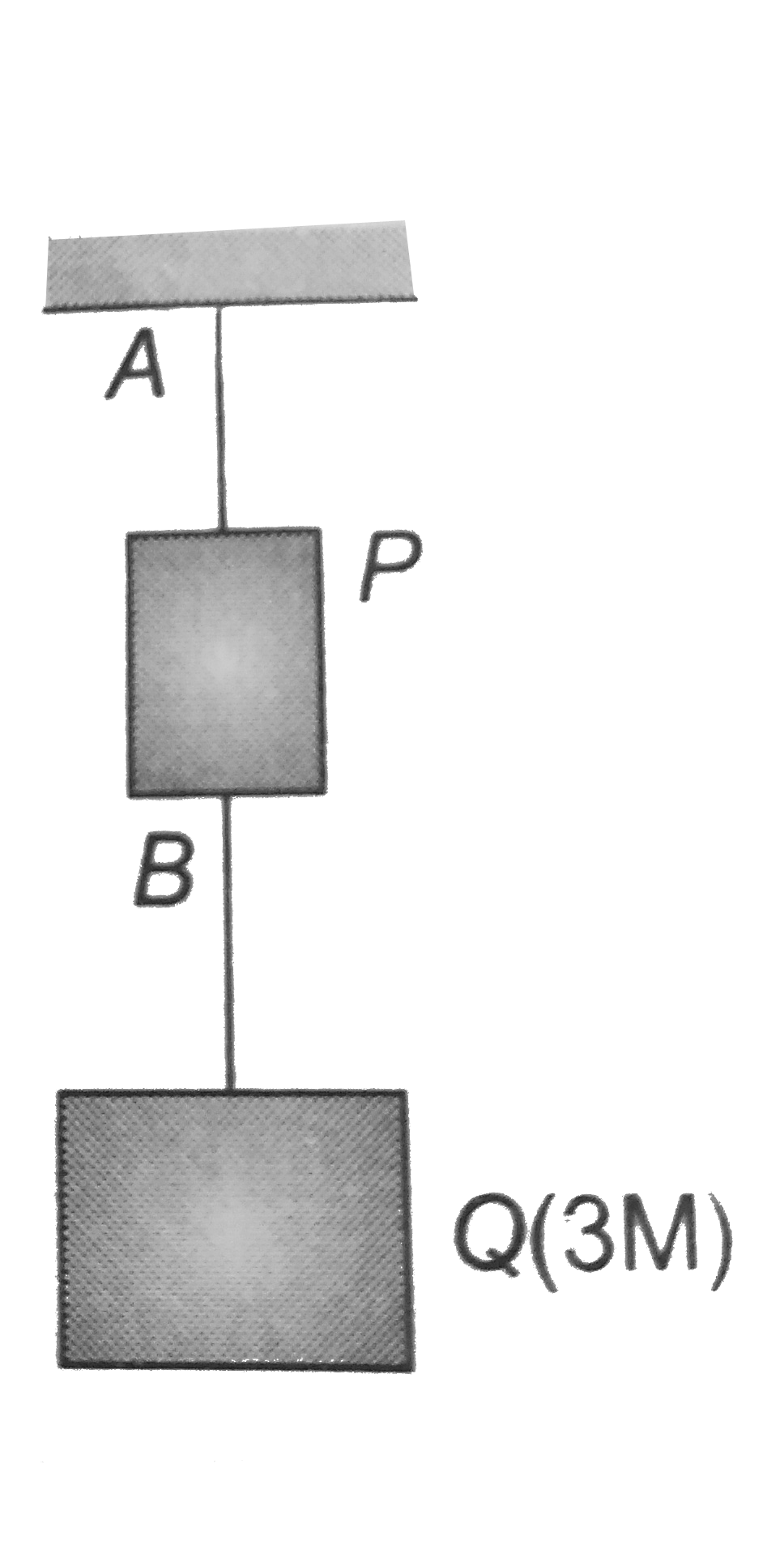
Wires A and B are connected with blocks P and Q, as shown, the ratio of lengths radii and Young's modulus of wires A and B are r, 2r and 3r respectively (r is a constant). Find the mass of block P if ratio of increase in their corresponding length is 16r2. The mass of the block Q is 3M
View SolutionThe radii and Young's moduli of two uniform wires A and B are in the ratio 2:1 and 1:2 respectively. Both wires are subjected to the same longitudinal force. If the increase in leangth of the wire A is one percent, the percentage increae in length of the wire B is
View SolutionThe ratio of the lengths of two wires A and B of same material is 1:2 and the ratio of their diameters is 2:1. They are stretched by the same force, then the ratio of increase in length will be
View SolutionTwo uniform brass rods A and B of lengths l and 2l and radii 2r and r respectively are heated to the same temperature. The ratio of the increase in the length of A to that of B is :
View Solution
