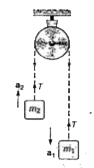
A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
8:1
9:7
4:3
5:3
The correct Answer is:B
a=(m1+m2)gm1+m2⇒g8=m1m2−1m1m2+1×g
⇒18(m1m2)+18=(m1m2−1)
⇒m1m2[18−1]=−1−18
m1m2=97
Similar Questions
A light string passing over a smooth light pulley connects two blocks of masses m_1 and m_2 (vertically). If the acceleration of the system is g/8 then the ratio of the masses is
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View SolutionTwo unequal masses m1 and m2 are connected by a string which passes over a frictionless and massless pulley. Find the tension in the string and the acceleration of the masses.
View SolutionTwo bodies with masses m_1 and m_2(m_1gtm_2) are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system (m_1+m_2) is
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View SolutionThe two bodies of mass m1andm2(m1>m2) respectively are tied to the ends of a massless string, which passes. over a light and frictionless pulley. The masses are initially at rest and then released. Then acceleration of the centre of mass of the system is
View Solution

