Two bodies with masses m1 and m2(m1>m2) are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system (m1+m2) is
(a) (m1−m2m1+m2)g
(b) (m1−m2m1+m2)2g
(c) m1gm1+m2
(d) m2gm1+m2
The correct Answer is:B
To find the acceleration of the center of mass of the system consisting of two bodies with masses m1 and m2 (where m1>m2), we can follow these steps:
Step 1: Identify the Forces Acting on the Masses
- The weight of mass m1 acting downward is m1g.
- The weight of mass m2 acting downward is m2g.
- The tension in the string acts upward on both masses.
Step 2: Write the Net Force Equation
The net force acting on the system can be expressed as:
Fnet=m1g−m2g
This is because m1 is heavier and will accelerate downward.
Step 3: Simplify the Net Force
We can factor out g:
Fnet=g(m1−m2)
Step 4: Determine the Total Mass of the System
The total mass M of the system is:
M=m1+m2
Step 5: Apply Newton's Second Law
According to Newton's second law, the net force is equal to the total mass times the acceleration a:
Fnet=Ma
Substituting the expressions we have:
g(m1−m2)=(m1+m2)a
Step 6: Solve for Acceleration a
Rearranging the equation to solve for a:
a=g(m1−m2)m1+m2
Step 7: Find the Acceleration of the Center of Mass
The acceleration of the center of mass aCM is the same as the acceleration a we derived:
aCM=g(m1−m2)m1+m2
Final Answer
Thus, the acceleration of the center of mass of the system is:
aCM=g(m1−m2)m1+m2
- The weight of mass m1 acting downward is m1g.
- The weight of mass m2 acting downward is m2g.
- The tension in the string acts upward on both masses.
The net force acting on the system can be expressed as:
Fnet=m1g−m2g
This is because m1 is heavier and will accelerate downward.
We can factor out g:
Fnet=g(m1−m2)
The total mass M of the system is:
M=m1+m2
According to Newton's second law, the net force is equal to the total mass times the acceleration a:
Fnet=Ma
Substituting the expressions we have:
g(m1−m2)=(m1+m2)a
Rearranging the equation to solve for a:
a=g(m1−m2)m1+m2
The acceleration of the center of mass aCM is the same as the acceleration a we derived:
aCM=g(m1−m2)m1+m2
Thus, the acceleration of the center of mass of the system is:
aCM=g(m1−m2)m1+m2
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Subjective
Explore 32 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Subjective Questions
Explore 1 Video
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Assertion And Reason
Explore 15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
Two bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.

View SolutionA pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
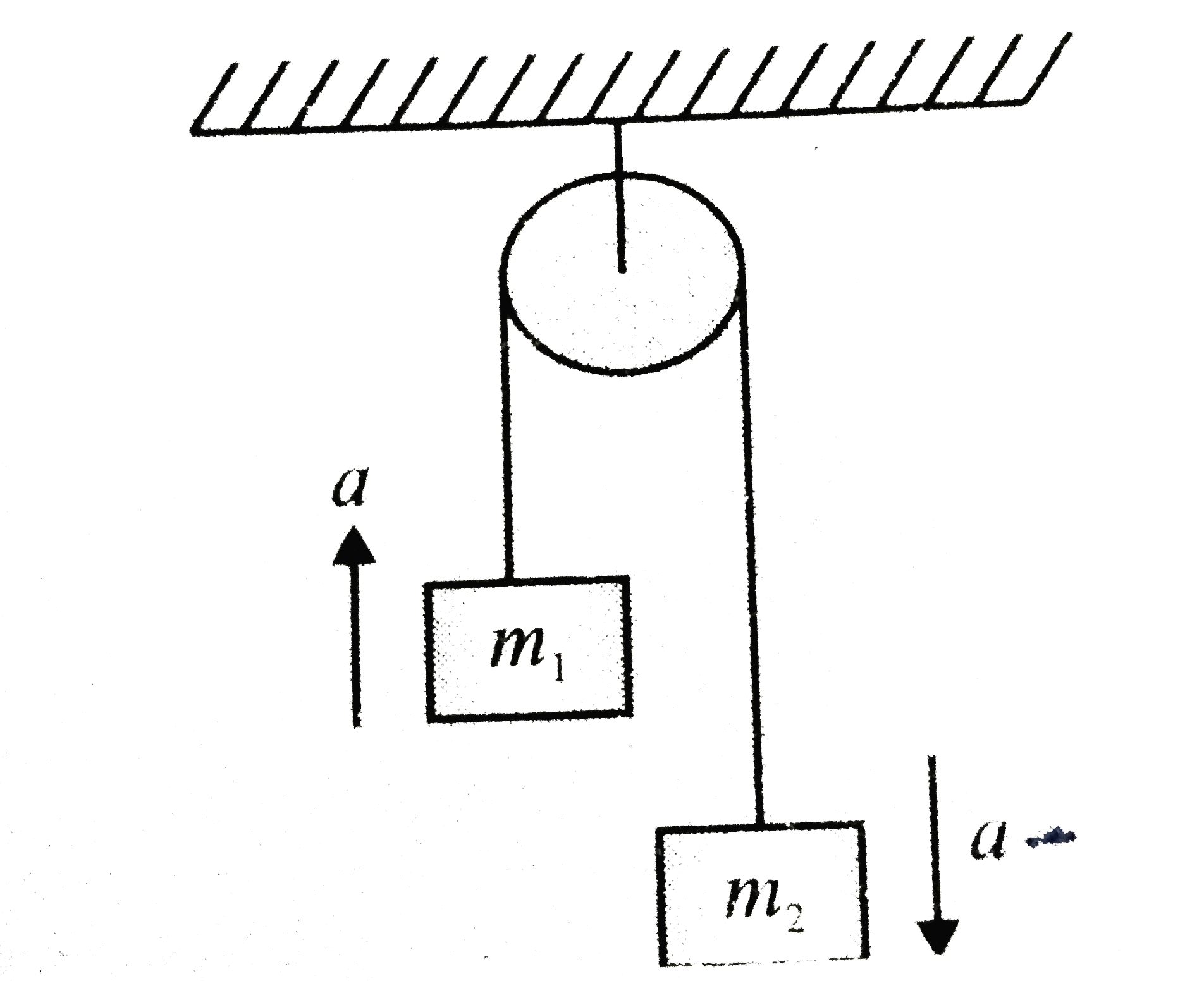
View SolutionTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)

View SolutionTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration

View SolutionTwo bodies of masses m1 and m2(m1>m2) respectively are tied to the ends j of a string which passes over a light frictionless pulley. The masses are intitially at rest and released. What is the acceleration of the centre of mass ?
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo particles of masses m and M(M>m) are connected by a cord that passes over a massless, frictionless pulley. The tension T in the string and the acceleration a of the particles is
View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View SolutionA pulley fixed to the ceiling of an elevator car carries a thread whose ends are attached to the masses m1andm2. The car starts going up with an acceleration a0. Assuming the masses of the pulley and the thread as well as the friction to be negligible, find:
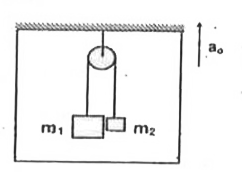
(a) the acceleration of the load m1 relative to the elevator shaft and relative to the car
(b) the force exerted by the pulley on the ceiling of the car. Given m1>m2.
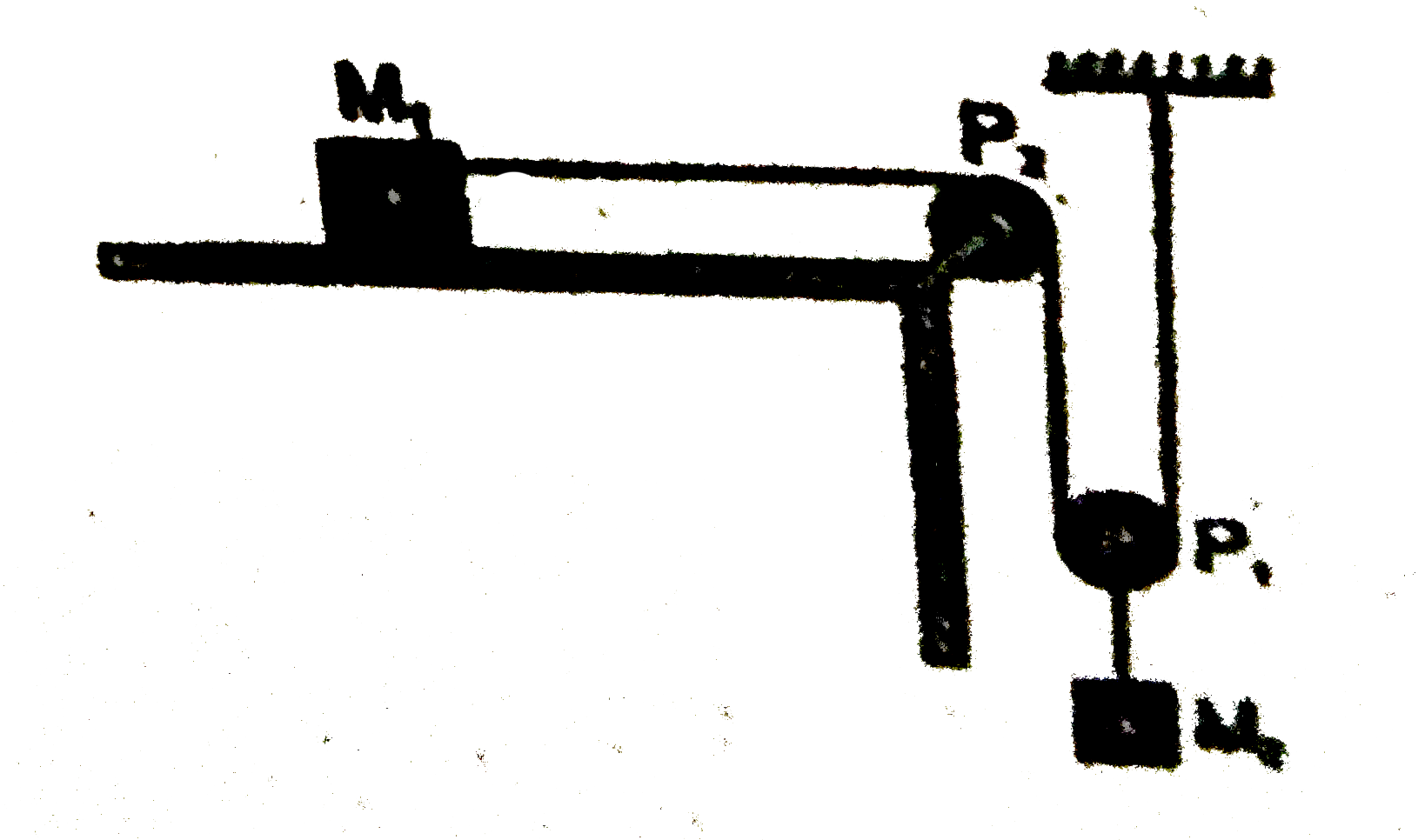
View SolutionBlocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
View Solution