A body is project at t= 0 with a velocity 10ms−1 at an angle of 60∘ with the horizontal .The readius of curvature of its trajectory at t=1s is R. Neglecting air resitance and taking acceleration due to gravity g=10ms−2, the value of R is :
2.8 m
2.5 m
10.3 m
5.1 m
The correct Answer is:A
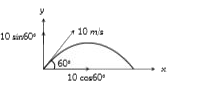
at t−1s,vy=5√3−10×1andvx=5
v=√25+(5√3−10)2
=√25+75+100−100√3=√200−100√3=5.11
rc=v2gcosθ=v2g(ux)v=v3gux=(5.11)310×5=2.77m
Similar Questions
A body is projected with velocity 24 ms−1 making an angle 30° with the horizontal. The vertical component of its velocity after 2s is (g=10ms−1 )
View SolutionA body is projected horizontally from a height of 78.4 m with a velocity 10 ms−1 . Its velocity after 3 seconds is [g = 10 ms−2] (Take direction of projection on →i and vertically upward direction on j)
View SolutionA body is project at t= 0 with a velocity 10ms−1 at an angle of 60∘ with the horizontal .The radius of curvature of its trajectory at t=1s is R. Neglecting air resitance and taking acceleration due to gravity g=10ms−2, the value of R is :
View SolutionA body is projected with velocity 24ms−1 making an angle 30∘ with the horizontal. The vertical component of its velocity after 2s is (g=10ms−1)
View SolutionA projectile thrown with an initial velocity of 10ms−1 at an angle a with the horizontal, has a range of 5 m . Taking g=10ms−2 and neglecting air resistance, what will be the estimated value of α ?
View SolutionA body is projected vertically upwards with a velocity of 10ms−1 and another body is projected simultaneously from the same point with a velocity of 20ms−1at an angle of π6 with the horizontal. The distance between the two bodies after one second from the time of projection is (Acceleration due to gravity is 10 ms^-2)
View SolutionA particle is projected horizontally form a tower with velocity 10ms−1. Taking g=10ms−2. Match the following two columns at time t = 1s.
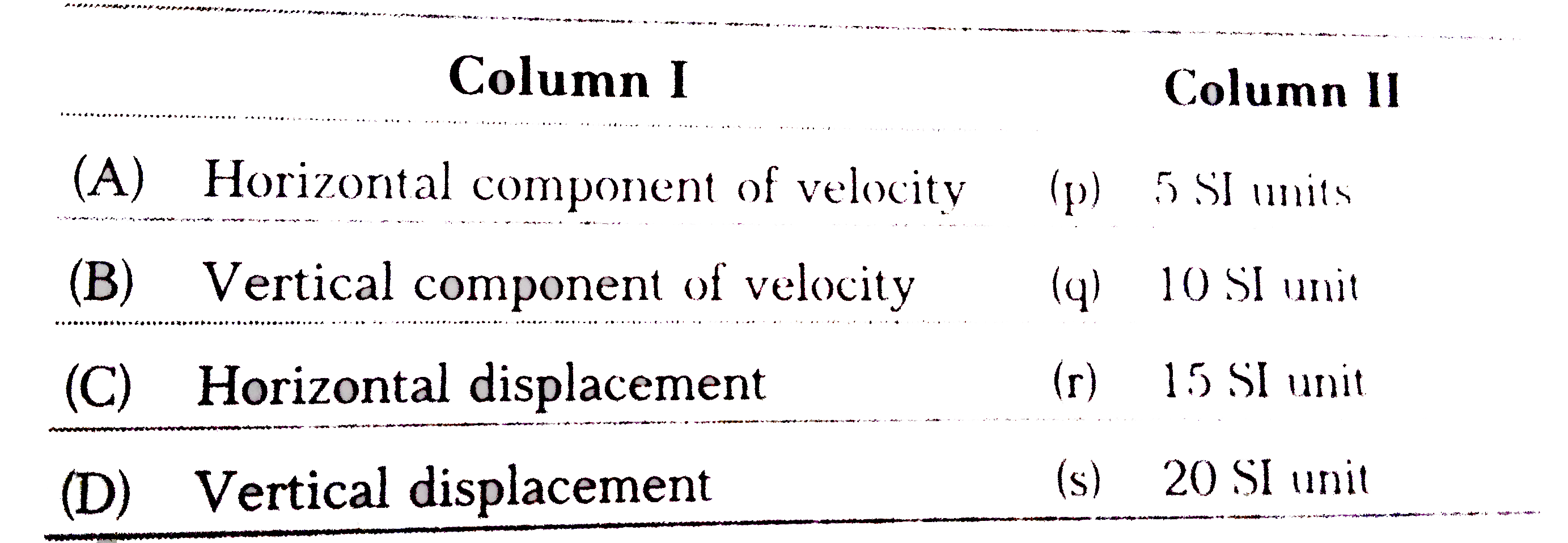
View SolutionA body is projected from height of 60 m with a velocity 10 ms^(-1) at angle 30^(0) is horizontal. The time of flight of the body is [g = 10ms^(-2)]
View Solution
