A particle is projected horizontally form a tower with velocity 10ms−1. Taking g=10ms−2. Match the following two columns at time t = 1s.
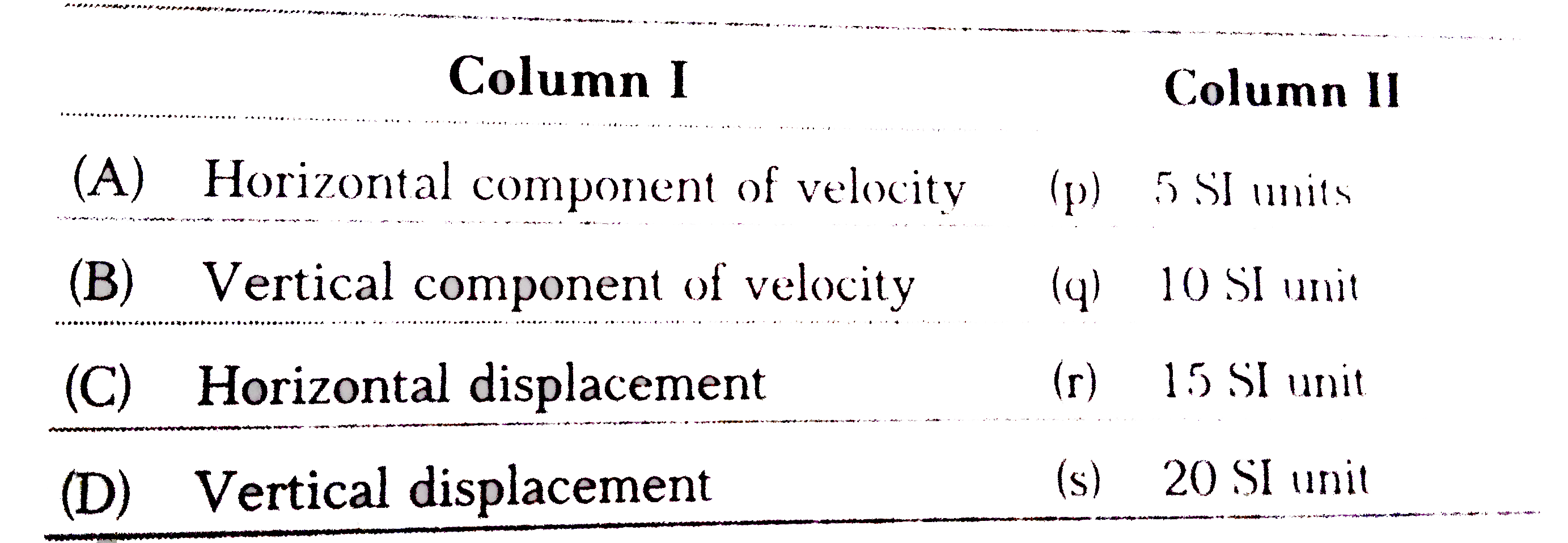
The correct Answer is:A→q,B→q,C→q,D→p
In horizontal projectile motion, Horizontal component of velocity ux=u=10ms−1
Vertical component of velocity uy=gt=10×1=10ms−1
Horizontal displacement =u×t=10×(1)=10m
Vertical displacement =12gt2=12×10×(1)2=5m
Topper's Solved these Questions
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:C. Medical entrances gallery
Explore 1 Video
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:Medical entrances gallery
Explore 19 Videos
- MOTIONBook:DC PANDEY ENGLISHChapter:MOTIONExercise:Medical entrance
Explore 12 Videos
- MEASUREMENT AND ERRORSBook:DC PANDEY ENGLISHChapter:MEASUREMENT AND ERRORSExercise:Subjective
Explore 19 Videos
- MOTION IN A PLANEBook:DC PANDEY ENGLISHChapter:MOTION IN A PLANEExercise:(C )Medical entrances gallery
Explore 32 Videos
Similar Questions
A stone is projected from the top of a tower with velocity 20ms−1 making an angle 30∘ with the horizontal. If the total time of flight is 5s and g=10ms−2
View SolutionA particle of mass 50 g is projected horizontally from the top of a tower of height 50 m with a velocity 20m/s. If g=10m/s2, then find the :-
View SolutionA particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
View SolutionA stone is projected horizontally with a velocity 9.8ms−1 from a tower of height 100 m. Its velocity one second after projection is (g=9.8ms−2).
View SolutionA particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.

View SolutionA body is projected horizontally from a height of 78.4 m with a velocity 10 ms−1 . Its velocity after 3 seconds is [g = 10 ms−2] (Take direction of projection on →i and vertically upward direction on j)
View SolutionA stone is projected vertically up from the ground with velocity 40ms−1 . The interval of time between the two instants at which the stone is at a height of 60 m above the ground is (g=10ms−2)
View SolutionA body is projected horizontally from the top of a tower with a velocity of 30 m/s. The velocity of the body 4 seconds after projection is (g = 10ms−2)
View SolutionA bullet is projected upwards from the top of a tower of height 90 m with the velocity 30ms−1 making an angle 30∘ with the horizontal. Find the time taken by it to reach the ground is (g=10ms−2)
View SolutionA body is projected at angle 30° to horizontal with a velocity 50 ms−1 . Its time of flight is (g=10 m/s2)
View Solution