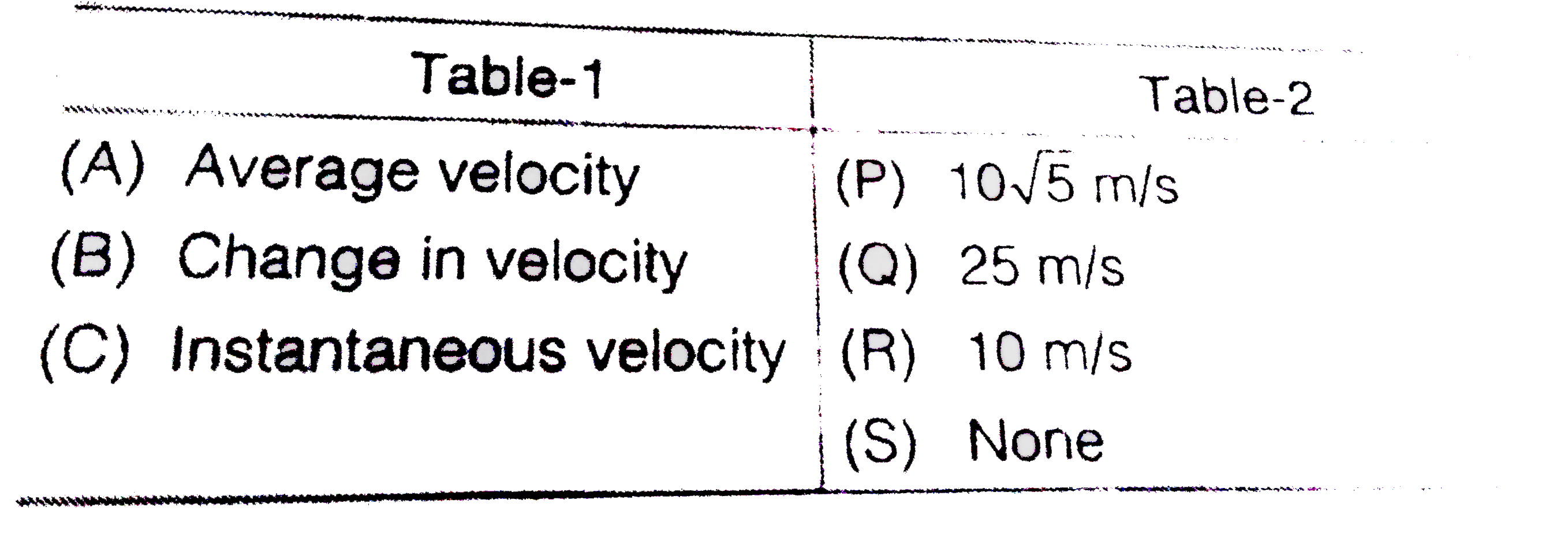A particle is projected horizontally form a tower with velocity 10ms−1. Taking g=10ms−2. Match the following two columns at time t = 1s.
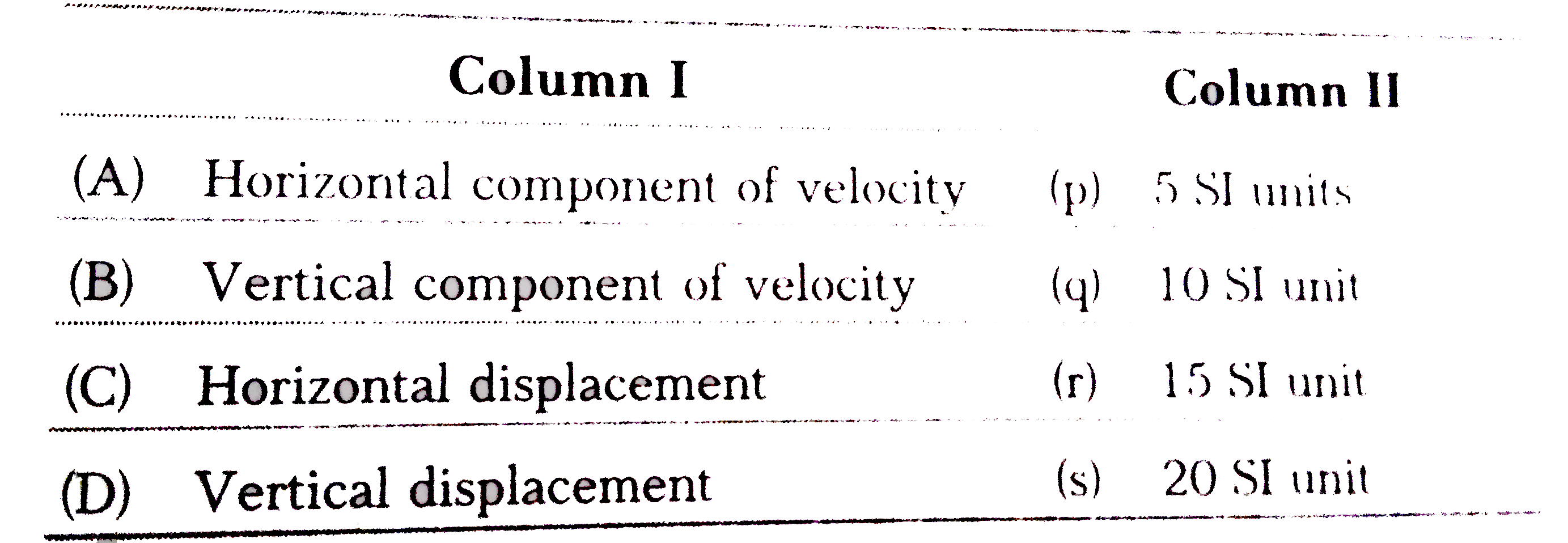
The correct Answer is:A→q,B→q,C→q,D→p
In horizontal projectile motion, Horizontal component of velocity ux=u=10ms−1
Vertical component of velocity uy=gt=10×1=10ms−1
Horizontal displacement =u×t=10×(1)=10m
Vertical displacement =12gt2=12×10×(1)2=5m
Topper's Solved these Questions
- MOTIONBook:DC PANDEYChapter:MOTIONExercise:C. Medical entrances gallery
Explore 1 Video
- MOTIONBook:DC PANDEYChapter:MOTIONExercise:Medical entrances gallery
Explore 19 Videos
- MOTIONBook:DC PANDEYChapter:MOTIONExercise:Medical entrance
Explore 12 Videos
- MEASUREMENT AND ERRORSBook:DC PANDEYChapter:MEASUREMENT AND ERRORSExercise:Subjective
Explore 19 Videos
- MOTION IN A PLANEBook:DC PANDEYChapter:MOTION IN A PLANEExercise:(C )Medical entrances gallery
Explore 32 Videos
Similar Questions
Knowledge Check
A particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
AAfter 2 s, the velocity of particle makes an angle of 60∘ with initial velocity vector.BAfter 1 s, the velocity of particles makes an angle of 60∘ with initial velocity vector.CThe magnitude of velocity of particle after 1 s is 10ms−1.DThe magnitude of velocity of particle after 1 s is 5ms−1.A particle is projected from a horizontal plane with a velocity of 8√2ms−1 ms at an angle θ. At highest point its velocity is found to be 8ms−1 Its range will be (g=10ms−2)
A3.2 mB4.6 mC6.4 mD12.8 mA stone is projected horizontally with a velocity 9.8ms−1 from a tower of height 100 m. Its velocity one second after projection is (g=9.8ms−2).
A9.8ms−1B4.9ms−1C9.8√2ms−1D4.9√2ms−1
A ball is projected horizontallu from a top of tower with a velocity of 10ms−1. Find the velocity of the ball after 0.5s.Take g= 10 ms^(-2).
View SolutionA particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.
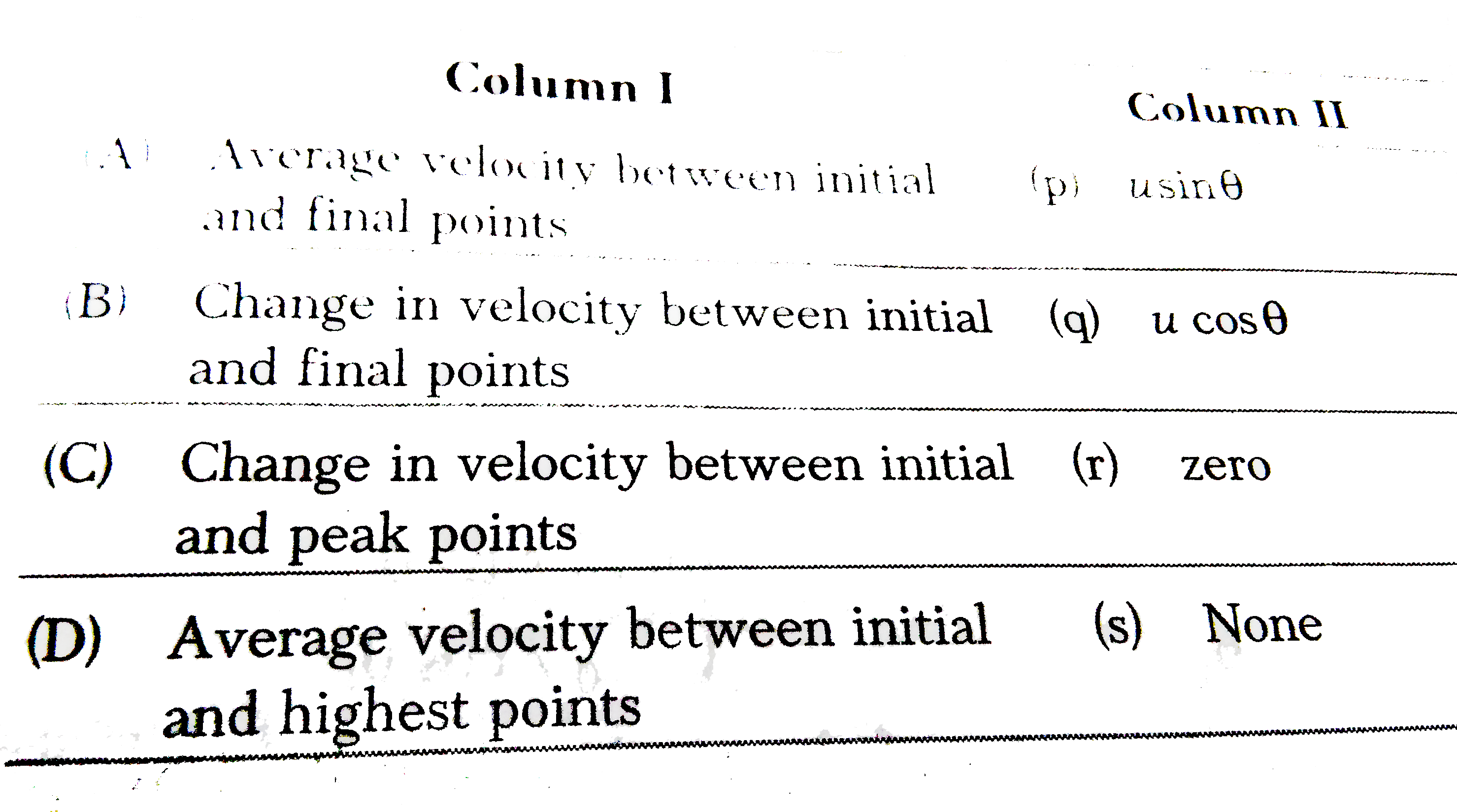
View SolutionA body is projected horizontally from the top of a tower of height 10m with a velocity 10m/s .Its velocity after 1 second is
View SolutionA body is projected horizontally from a height of 78.4m with a velocity 10ms−1.Its velocity after 3seconds is (g=10m/s2) (Take direction of projection as i and vertically upward direction as j)
View SolutionA particle is projected with initial velocity of ˆi+2ˆj. The equation of trajectory is (takeg=10ms−2)
View Solution