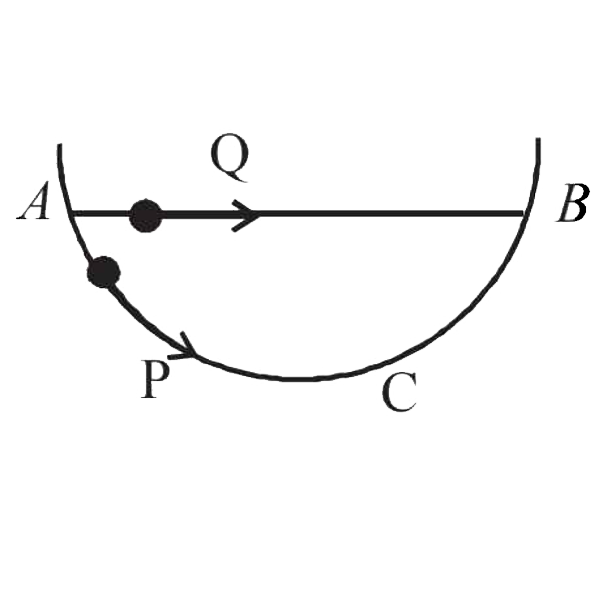
A particle P is sliding down a frictionless hemispherical bowl. It passes the point A at t=0. At this instant of time, the horizontal component of its velocity is v. A bead Q of the same mass as P is ejected from A at t=0 along the horizontal string AB, with the speed v. Friction between the bead and the string may be neglected. Let tP and tQ be the respective times taken by P and Q to reach the point B. Then:
tP<tQ
tP=tQ
tP>tQ
All of these
The correct Answer is:A
At point A speed of both the masses is same vQ→ remains the same in horizontal direction as no force is acting in this direction . For P the horizontal velocity 1st increases due to N sin θ reaches max value at O and then decrease

Thus, vP≥vQ,tP<tQ
Similar Questions
एक कण P घर्षण रहित अर्धगोलाकार प्याले (Hemispherical blow ) में तली ( निचे ) की ओर फिसल रहा है। यह संभव t =0 पर बिंदु A से गुजरता है। इस क्षणिक समय t में कम के वेग का क्षैतिज घटक V है। P के बराबर द्रव्यमान की ओर मणिक (Bead ) Q ,t =0 समय पर A से धागे AB के अनुदिश v चाल से चलना प्रारम्भ करता है। माणिक तथा धागे के बीच घर्षण नगण्य माना जाता है। यदि tp तथा tQ क्रमशः P तथा Q को बिंदु B तक पहुंचने में लगे समय हो, तब

View SolutionA bead can slide on a smooth straight wire and a particle of mass m attached to the bead by a light string of length L . The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass 2m then when the string makes an angle theta with the wire, the bead will have slipped a distance.
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA particle P is sliding down a frictionless hemispherical bowl. It passes the point A at t=0 . At this instant of time, the horizontal component of its velocity is v. A bead Q of the same mass as P is ejected from A at t=0 along the horizontal string AB, with the speed v. Friction between the bead and the string may be neglected. Let t_P and t_Q be the respective times taken by P and Q to reach the point B. Then:
View SolutionA positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.
View SolutionA particle P is sliding down a frictionless hemispherical bowl. It passes the point A at t=0. At this instant of time, the horizontal component of its velocity is v. A bead Q of the same mass as P is ejected from A at t=0 along the horizontal string AB, with the speed v. Friction between the bead and the string may be neglected. Let tP and tQ be the respective times taken by P and Q to reach the point B. Then:

View SolutionA bead can slide on asmooth straight wire and a particle of mass m attached to the bead by a light string of length L. The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass 2m then when the string makes an angle θ with the wire, the bead will have slipped a dsitance.

View SolutionA bead is connected with a fixed disc of radius R by an inextensible massless string in a smooth horizontal plane. If the bead is pushed with a velocity v_(0) prependicular to the string, the bead moves in a curve and consequently collapses on the disc. Then
View Solution
