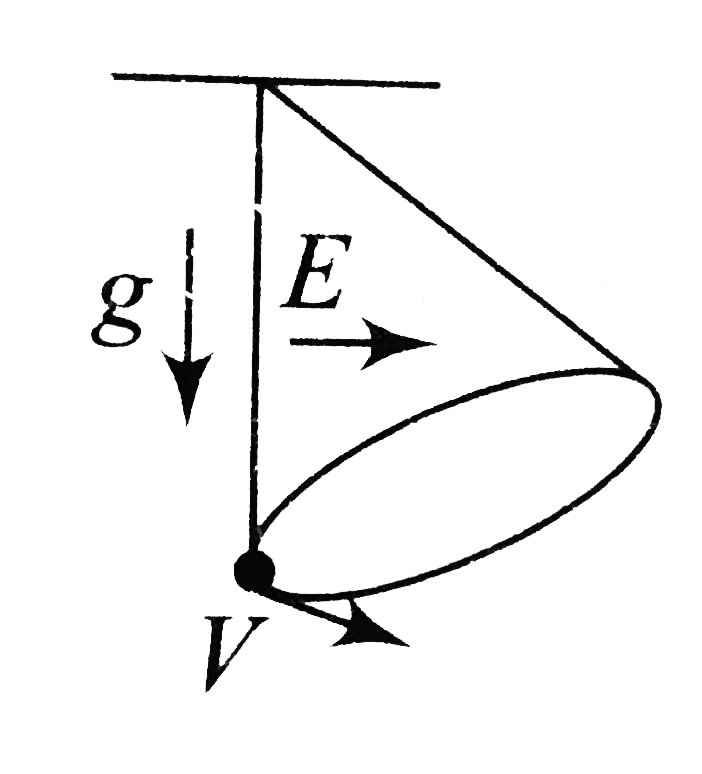
A positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.
2qEm(√lg)
qEm(√lg)
qEm(√2lg)
qE2m(√lg)
The correct Answer is:B
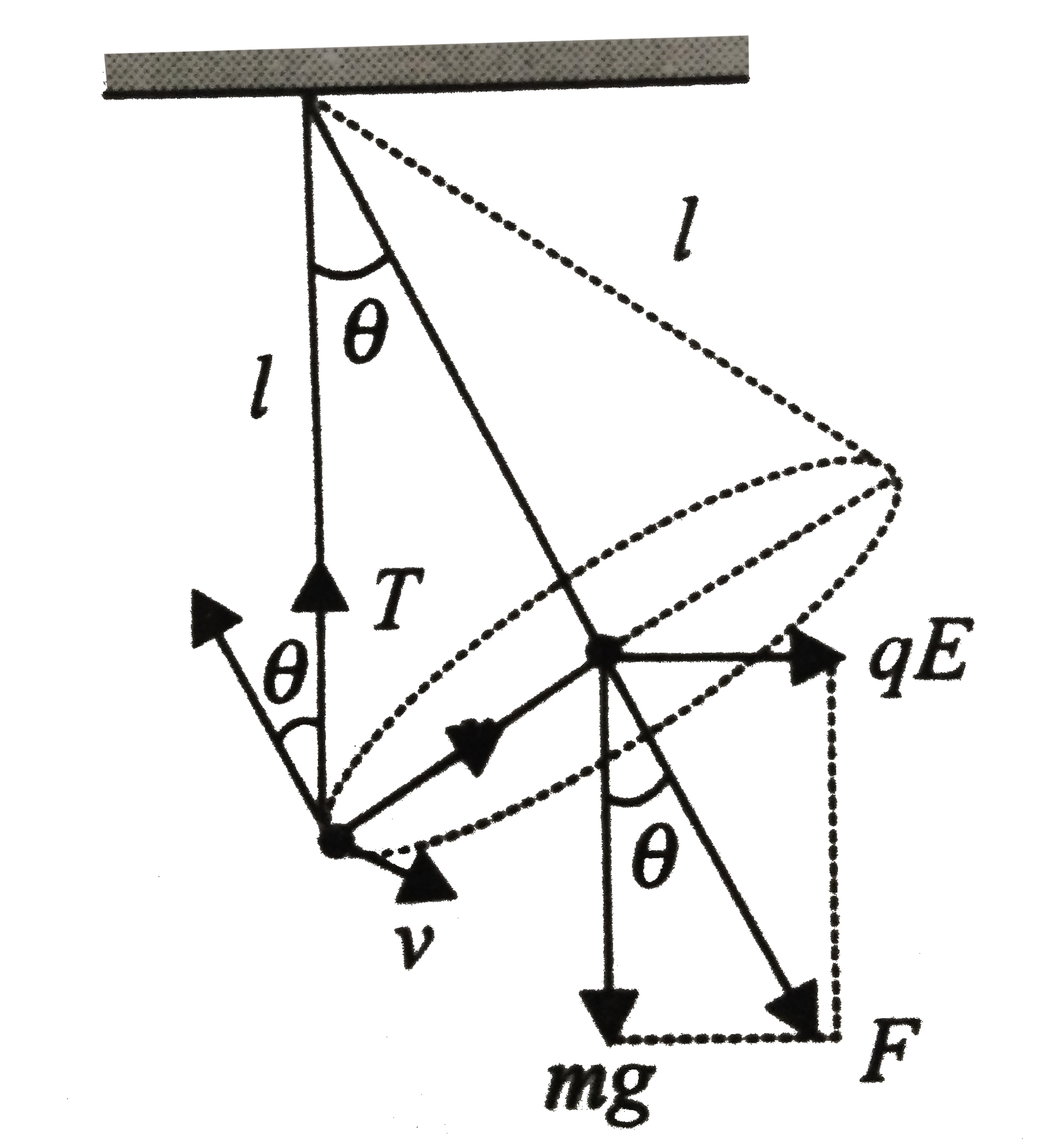
b. θ is equilibrium position. Net force in equilibrium position
F=√(mg)2+(qE)2
tanθ=qEmg
Tcosθ=F
Tsinθ=mv2r
where r=lsinθ
Solve to get v=qEm√lg
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Multiple Correct Answer type
109 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - CENGAGE PHYSICSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Question Bank
4 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
A particle of mass m=0.1kg and having positive charge q=75μC is suspended from a point by a thread of length l=10cm. In the space, a uniform horizontal electric field E=104NC−1 exists. The particle is drawn aside so that the thread becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with the same constant speed V. Calculate the radius of the circle and speed v(g=10ms−2).
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r such that r =L√2. The speed of particle will be :
View Solution
Knowledge Check
A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
Arg√L2−r2Br√g(L2−r2)14Cr√g(L2−r2)12DmgL(L2−r2)12A particle of mass m is suspended from a string of length l fixed to the point O. What velocity should be imparted to the particle in its lowermost position so that the string is just able to reach the horizontal diameter of the circle?
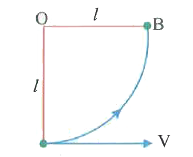 Av=√2glBv=√3glCv=√glDv=2gl
Av=√2glBv=√3glCv=√glDv=2glA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
A√TlmB√2TlmC√3TlmD√Tml
A particle is having mass m & charge +q is projected horizontally from point O. Electric field is present and is directed vertically downward .
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
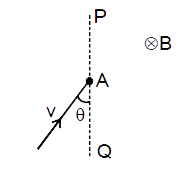
distance travelled in the magnetic field
View SolutionA particle having mass m and charge q is projected at an angle of 75° to the horizontal with a speed u. A uniform electric field E=mgq exists in horizontal direction. Find the time after projection when the velocity of particle makes an angle of 45° with horizontal.
View SolutionA paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are

View SolutionA particle of charge q and mass m, is fired perpenducular to a magnetic field (B) with a velocity v. What is the frequency of revolution of the particle?
View Solution
