A particle P is sliding down a frictionless hemispherical bowl. It passes the point A at t = 0. At this instant of time, the horizontal component of its velocity is v. A bead Q of the same mass as P is ejected from A at t = 0 along the horizontal string AB, with a speed v. Friction between the bead and the string may be neglected. Let tP and tQ be the respective times taken by P and Q to reach the point B. Then:
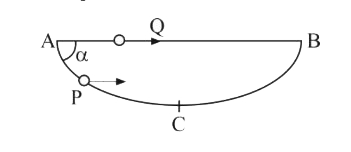
tp<tQ
tp=tQ
tp>tQ
tptQ=Length of areACBLength ofAB
The correct Answer is:a
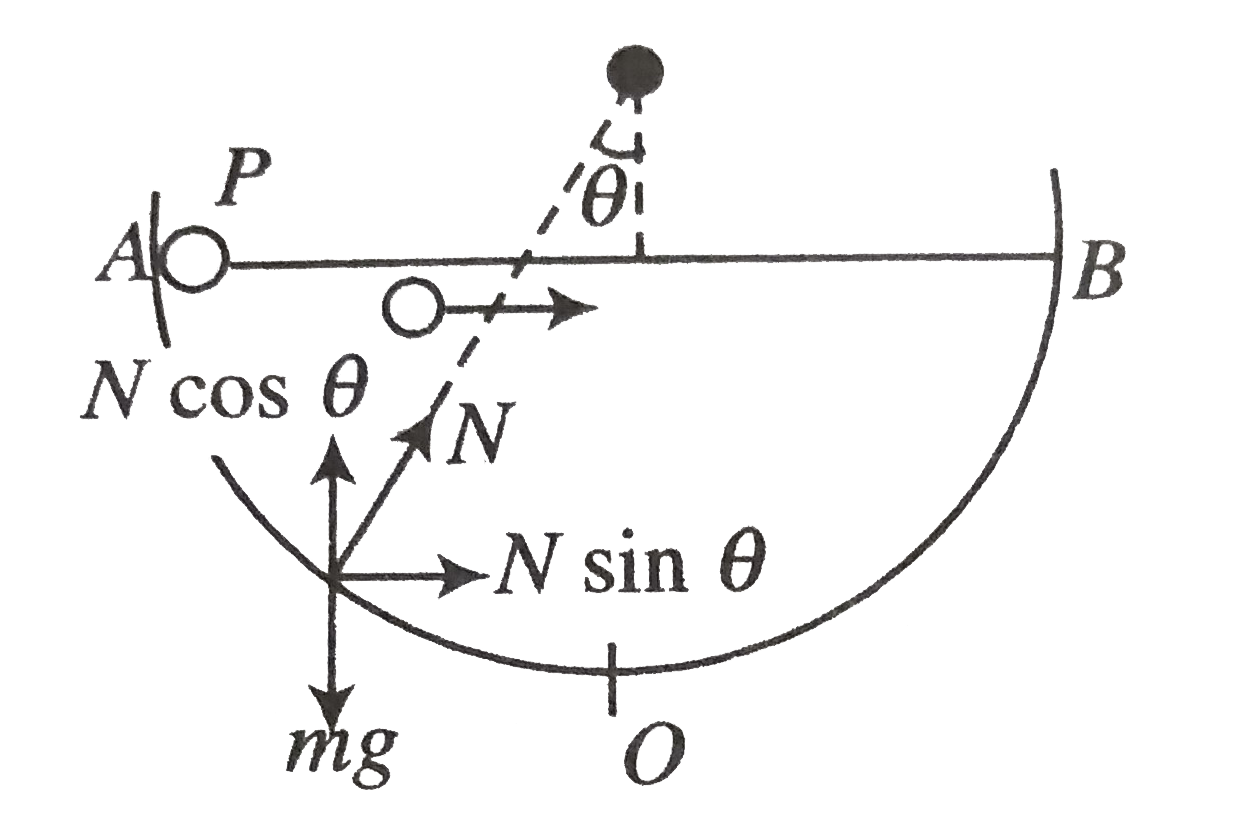
As A the horizontal speeds of both the masses is the same .The velocity of Q remain the same horizontal as so force it acting on the horizontal dipection but it case of P as shown at any internadiate position the horizontal velocity first increase (the as Nsinθ) reaches a maximum value at O and then decreases this it always remain greater than v Therefore tp<tQ
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Assertion -reasoning
Explore 2 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Single correct answer type
Explore 13 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
A particle P is sliding down a frictionless hemispherical bowl. It passes the point A at t=0. At this instant of time, the horizontal component of its velocity is v. A bead Q of the same mass as P is ejected from A at t=0 along the horizontal string AB, with the speed v. Friction between the bead and the string may be neglected. Let tP and tQ be the respective times taken by P and Q to reach the point B. Then:
View SolutionA particle P is sliding down a frictionless hemispherical bowl. It passes the point A at t = 0. At this instant of time, the horizontal component of its velocity is v. A bead Q of the same mass as P is ejected from A at t = 0 along the horizontal string AB, with a speed v. Friction between the bead and the string may be neglected. Let tP and tQ be the respective times taken by P and Q to reach the point B. Then:

View SolutionA particle is projected with a speed v and an angle θ to the horizontal. After a time t, the magnitude of the instantaneous velocity is equal to the magnitude of the average velocity from 0 to t. Find t.
View SolutionA particle is projected horizontally as shown from the rim of a large hemispherical bowl. The displacement of the particle when it strikes the bowl the first time is R. Find the velocity of the particle at that instant and the time taken.

View SolutionA particle is projected at time t=0 from a point P wilth a speed v0 at an angle of 45∘ to the horizontal. Find the magnitude and the direction of the angular momentum of the particle about the point P at time t=v0g
View SolutionA particle moves move on the rough horizontal ground with some initial velocity V0. If 34 of its kinetic enegry lost due to friction in time t0. The coefficient of friction between the particle and the ground is.
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA disc is rolling without slipping on a horizontal surface with C, as its centre and Q and P the two points equidistant from C. Let vP,vQandvC be the magnitudes of velocities of point P,Q and C respectively, then

View Solution

