A particle moves move on the rough horizontal ground with some initial velocity V0. If 34 of its kinetic enegry lost due to friction in time t0. The coefficient of friction between the particle and the ground is.
v02gt0
v04gt0
3v04gt0
v0gt0
The correct Answer is:A
To solve the problem step by step, we can follow these steps:
Step 1: Determine Initial and Final Kinetic Energy
The initial kinetic energy (KE_initial) of the particle can be expressed as:
KEinitial=12mV20
According to the problem, three-fourths of the kinetic energy is lost due to friction, meaning that the final kinetic energy (KE_final) is:
KEfinal=KEinitial−34KEinitial=14KEinitial
Step 2: Express Final Kinetic Energy
Substituting the expression for KE_initial into the equation for KE_final:
KEfinal=14(12mV20)=18mV20
Step 3: Relate Final Kinetic Energy to Final Velocity
The final kinetic energy can also be expressed in terms of the final velocity V′:
KEfinal=12mV′2
Setting the two expressions for KE_final equal gives:
12mV′2=18mV20
We can cancel m from both sides (assuming m≠0):
12V′2=18V20
Step 4: Solve for Final Velocity
Multiplying both sides by 2:
V′2=14V20
Taking the square root:
V′=V02
Step 5: Determine the Acceleration
The acceleration a due to friction can be expressed as:
a=−μg
where μ is the coefficient of friction and g is the acceleration due to gravity.
Step 6: Use the Equation of Motion
Using the equation of motion:
V′=V0+at
Substituting the known values:
V02=V0−μgt0
Rearranging gives:
μgt0=V0−V02=V02
Step 7: Solve for the Coefficient of Friction
Now, we can solve for μ:
μgt0=V02
μ=V02gt0
Final Answer
The coefficient of friction μ between the particle and the ground is:
μ=V02gt0
---
The initial kinetic energy (KE_initial) of the particle can be expressed as:
KEinitial=12mV20
According to the problem, three-fourths of the kinetic energy is lost due to friction, meaning that the final kinetic energy (KE_final) is:
KEfinal=KEinitial−34KEinitial=14KEinitial
Substituting the expression for KE_initial into the equation for KE_final:
KEfinal=14(12mV20)=18mV20
The final kinetic energy can also be expressed in terms of the final velocity V′:
KEfinal=12mV′2
Setting the two expressions for KE_final equal gives:
12mV′2=18mV20
We can cancel m from both sides (assuming m≠0):
12V′2=18V20
Multiplying both sides by 2:
V′2=14V20
Taking the square root:
V′=V02
The acceleration a due to friction can be expressed as:
a=−μg
where μ is the coefficient of friction and g is the acceleration due to gravity.
Using the equation of motion:
V′=V0+at
Substituting the known values:
V02=V0−μgt0
Rearranging gives:
μgt0=V0−V02=V02
Now, we can solve for μ:
μgt0=V02
μ=V02gt0
The coefficient of friction μ between the particle and the ground is:
μ=V02gt0
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRANCE SPECIAL QUESTIONS
16 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MATCH THE COLUMNS
7 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.3
10 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
A particle is projected directly along a rough plane of inclination θ with velocity u. If after coming to the rest the particle returns to the starting point with velocity v, the coefficient of friction between the partice and the plane is
View SolutionAsseration : A block of mass m starts moving on a rough horizontal surface with a velocity v. It stops due to friction between the block and the surface after moving through a ceratin distance. The surface is now tilted to an angle of 30∘ with the horizontal and same block is made to go up on the surface with the same initial velocity v. The decrease in the mechanical energy in the second situation is small than the first situation.
Reason : The coefficient of friction between the block and the surface decreases with the increase in the angle of inclination.
View SolutionA block starts moving up an inclined plane of inclination 30∘ with an initial velocity of v0 . It comes back to its initial position with velocity v02 . The value of the coefficient of kinetic friction between the block and the inclined plane is close to I1000 , The nearest integer to I is ____________ .
View SolutionA positively charged particle of mass m and charge q is projected on a rough horizontal x-y plane surface with z-axis in the vertically upward direction. Both electric and magnetic fields are acting in the region and given by →E=−E0ˆkand→B=−B0ˆk , respectively. The particle enters into the field at (a0,0,0) with velocity →v=v0ˆj. The particle starts moving in some curved path on the plane. If the coefficient of friction between the particle and the plane is μ. Then calculate the
(a) time when the particle will come to rest
(b) distance travelled by the particle when it comes to rest.

View SolutionA positively charged particle of mass m and charge q is projected on a rough horizontal x-y plane surface with z-axis in the vertically upward direction. Both electric and magnetic fields are acting in the region and given by →E=−E0ˆkand→B=−B0ˆk , respectively. The particle enters into the field at (a0,0,0) with velocity →v=v0ˆj. The particle starts moving in some curved path on the plane. If the coefficient of friction between the particle and the plane is μ. Then calculate the
(a) time when the particle will come to rest
(b) distance travelled by the particle when it comes to rest.

View SolutionA uniform ring of mass 'm' and radius 'R' is projected horizontally with velcoty v0 on a rough horizontal floor, so that it starts off with a purely sliding motion and it acquires a pure rolling motion after moving a distance d. If the coefficient of friction between the ground and ring is μ, then work done by the friction in the process is
View SolutionWhen a car of 3mass 1000 kg is moving with a velocity of 20ms−1 on a rough horizontal road, its engine is switched off. How far does the car move before it comes to rest if the coefficient of kinetic friction between the road and tyres of the car is 0.75 ?
View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.
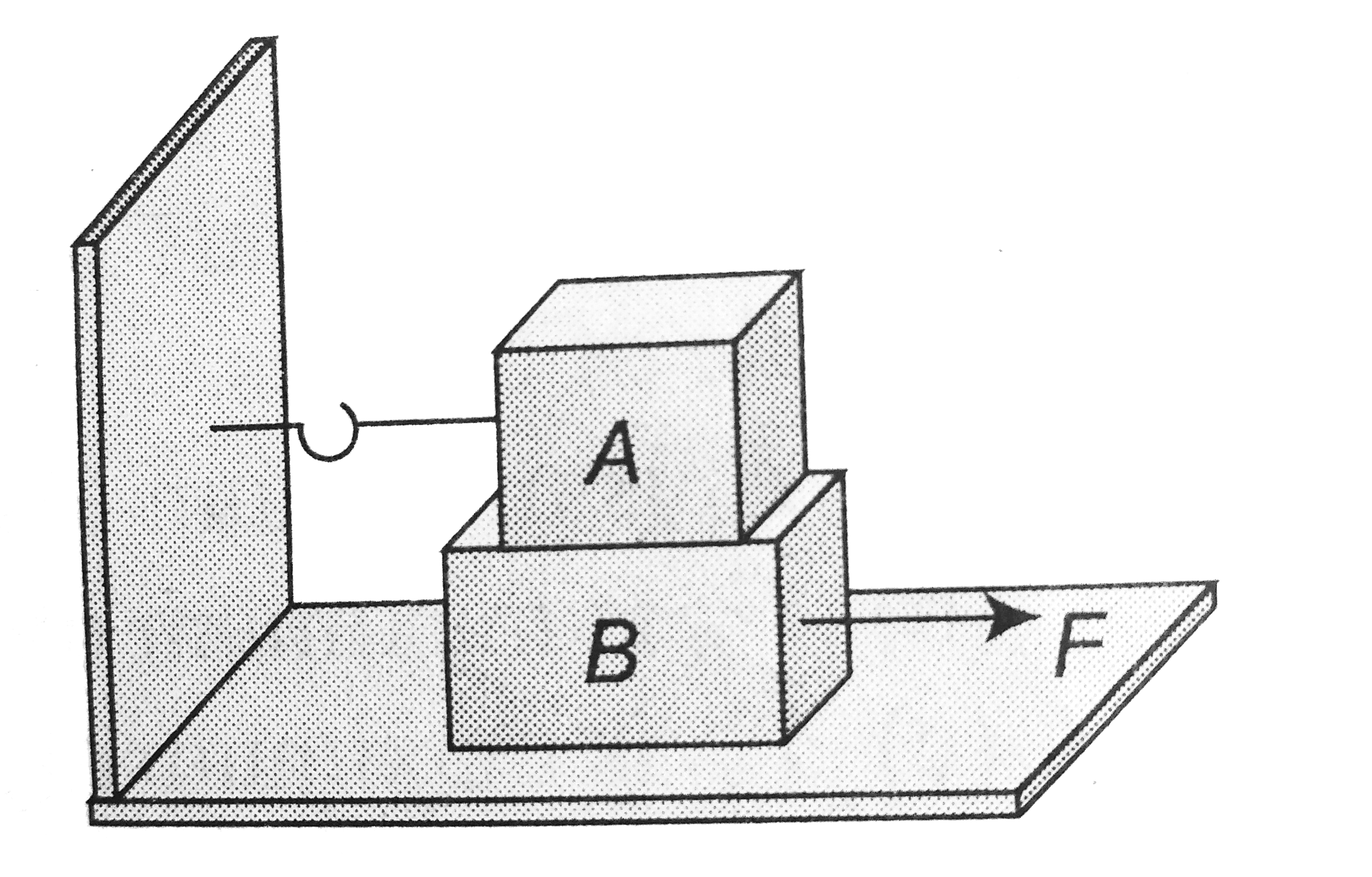
View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

View SolutionA block A with mass 100kg is resting on another block B of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3 . the minimum required force F to start moving B will be.

View Solution
