A concave mirror of radius of curvature R has a circular outline of radius r. A circular disc is to be placed normal to the axis at the focus so that it collects all the light that is reflected from the mirror from a beam parallel to the axis. For r >>R, the area of this disc has to be at least
πr64R4
πr64R2
πr54R3
πr4R2
The correct Answer is:A
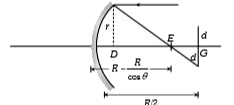
d → Radius of disc
A = πd2
From similar triangle
rd=R−R2cosθR2−(R−R2cosθ)⇒rd=2cosθ−1−cosθ+1
⇒d=(−cosθ+12cosθ+1)r
sinθ=rR,cosθ=√R2−r2R
cosθ=(1−r2R2)12=1−12r2R2
(Using Binomial expansion )
1−cosθ=r22R2
d=r2×r2R2[2(1−r22R2)−1]⇒d=r32R2
Area (A) = πd2=πr64R4.
Topper's Solved these Questions
- RAY OPTICSBOOK - ERRORLESSCHAPTER - RAY OPTICSEXERCISE - NCERT BASED QUESTIONS (Refraction of Light at Plane Surfaces)
48 Videos
- RAY OPTICSBOOK - ERRORLESSCHAPTER - RAY OPTICSEXERCISE - NCERT BASED QUESTIONS ( Total internal reflection )
26 Videos
- RAY OPTICSBOOK - ERRORLESSCHAPTER - RAY OPTICSEXERCISE - Assertion & Reason
30 Videos
- MAGNETISMBOOK - ERRORLESSCHAPTER - MAGNETISMEXERCISE - Assertion and Reason
22 Videos
- WAVE OPTICS AND ELECTROMAGNETIC THEORYBOOK - ERRORLESSCHAPTER - WAVE OPTICS AND ELECTROMAGNETIC THEORYEXERCISE - ASSERTION & REASON
27 Videos
Similar Questions
Knowledge Check
The moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is.
A12MR2BMR2C25MR2D32MR2The radius of gyration of a uniform circular disc of radius R, about any diameter of the disc is
AK=RBK=R/2CK=2RDnone of theseA disc of radius R has a concentric hole of radius r. It is floating on a liquid of surface tension T . What is the force of surface tension on the disc ?
A4π(R+r)TB4π(R−r)TC2π(R−r)TD2π(R+r)T
A circular metallic disc of radius R has a small circular cavity of radius r as shown in figure. On heating the system :

View SolutionConcave mirror object at d1 from curvature of radius R and image at d2 from C. Then,
View SolutionFrom a uniform circular disc of radius R, a circular disc of radius R/6 and having centre at a distance R/2 from the centre of the disc is removed. Determine the centre of mass of remaining portion of the disc.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View SolutionFrom the circular disc of radius 4R two small discs of radius R are cut off. The centre of mass of the new structure will be at
View Solution

