Concave mirror object at from curvature of radius R and image at from C. Then,
To solve the problem regarding the relationship between the object distance d1 from the center of curvature C and the image distance d2 from C for a concave mirror, we can follow these steps:
1. Understand the Setup:
- We have a concave mirror with a center of curvature C and a radius of curvature R. The object is placed at a distance d1 from C and the image is formed at a distance d2 from C.
2. Identify Distances:
- The object distance u is measured from the pole P of the mirror. Since the object is on the left side of the mirror, we write:
u=−(R+d1)
- The image distance v from the pole is:
v=R−d2
3. Focal Length:
- The focal length f of a concave mirror is given by:
f=−R2
4. Apply the Mirror Formula:
- The mirror formula is given by:
1f=1v+1u
- Substituting the values of f, u, and v:
−2R=1R−d2+1−(R+d1)
5. Simplify the Equation:
- Rearranging gives:
−2R=1R−d2−1R+d1
- Finding a common denominator for the right side:
−2R=(R+d1)−(R−d2)(R−d2)(R+d1)
- This simplifies to:
−2R=d2+d1(R−d2)(R+d1)
6. Cross-Multiply and Rearrange:
- Cross-multiplying gives:
−2(R−d2)(R+d1)=Rd2+Rd1
- Expanding and simplifying leads to:
−2R2+2Rd2+2Rd1−2d1d2=Rd2+Rd1
- Rearranging terms results in:
2d1d2=R(d1+d2)
7. Final Relation:
- Dividing both sides by d1−d2 gives the final relation:
R=2d1d2d1−d2
- We have a concave mirror with a center of curvature C and a radius of curvature R. The object is placed at a distance d1 from C and the image is formed at a distance d2 from C.
- The object distance u is measured from the pole P of the mirror. Since the object is on the left side of the mirror, we write:
u=−(R+d1)
- The image distance v from the pole is:
v=R−d2
- The focal length f of a concave mirror is given by:
f=−R2
- The mirror formula is given by:
1f=1v+1u
- Substituting the values of f, u, and v:
−2R=1R−d2+1−(R+d1)
- Rearranging gives:
−2R=1R−d2−1R+d1
- Finding a common denominator for the right side:
−2R=(R+d1)−(R−d2)(R−d2)(R+d1)
- This simplifies to:
−2R=d2+d1(R−d2)(R+d1)
- Cross-multiplying gives:
−2(R−d2)(R+d1)=Rd2+Rd1
- Expanding and simplifying leads to:
−2R2+2Rd2+2Rd1−2d1d2=Rd2+Rd1
- Rearranging terms results in:
2d1d2=R(d1+d2)
- Dividing both sides by d1−d2 gives the final relation:
R=2d1d2d1−d2
Topper's Solved these Questions
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-A
Explore 80 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-B
Explore 40 Videos
- JEE MAINBook:JEE MAINS PREVIOUS YEARChapter:JEE MAINExercise:All Questions
Explore 473 Videos
- JEE MAIN 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2022Exercise:Question
Explore 492 Videos
Similar Questions
Knowledge Check
An object is placed at a large distance in front of a convex mirror of radius of curvature 40 cm . What is the distance of image from the mirror ?
A40 cmB20 cmC60 cmD80 cmAn object ABED is placed in front of a concave mirror beyond the center of curvature C as shown in figure., State the shape of the image.
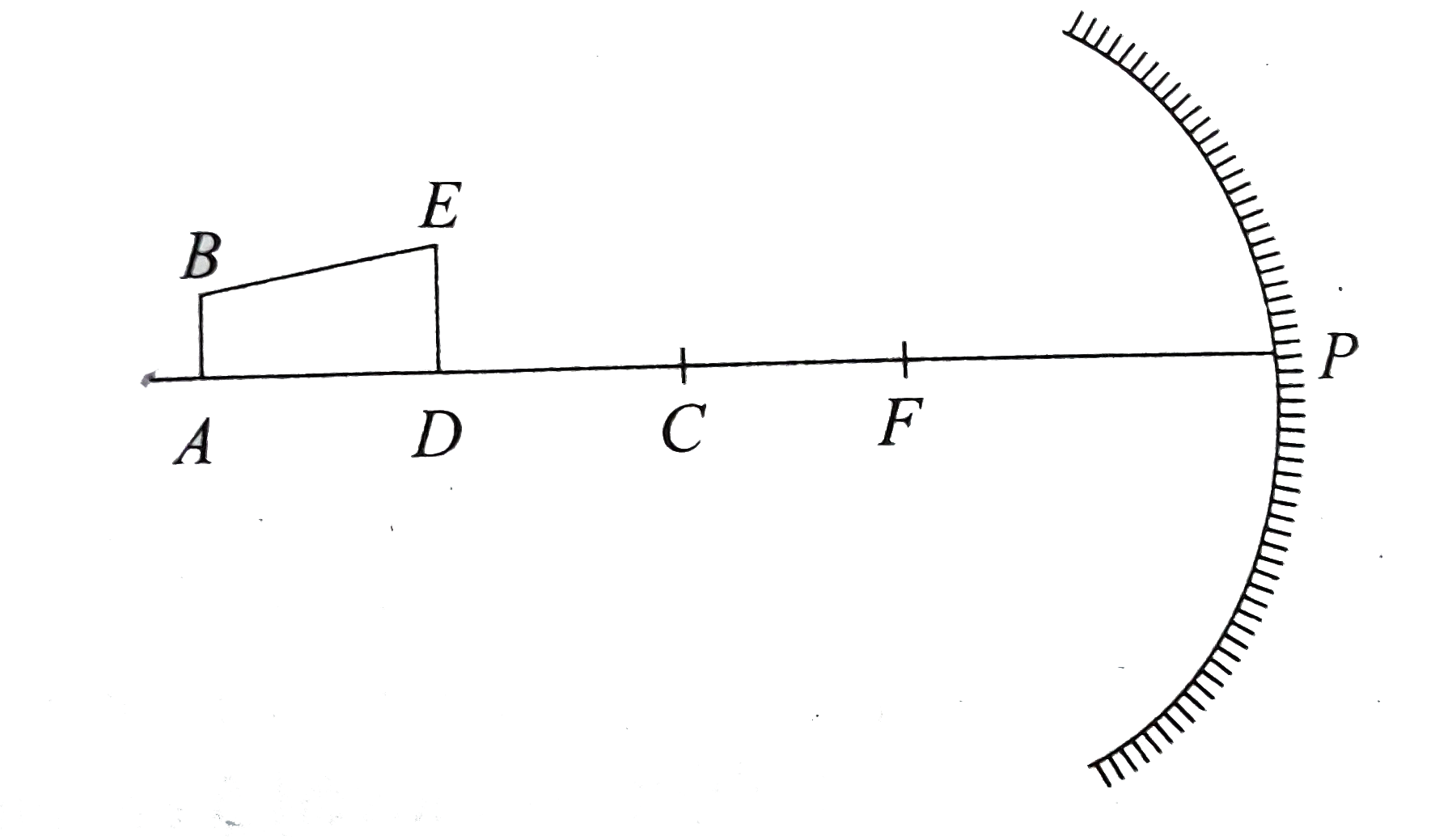 A|mAB|<1and|mED|<1B|mAB|>1and|mED|<1C|mAB|<1and|mED|>1D|mAB|>1and|mED|>1
A|mAB|<1and|mED|<1B|mAB|>1and|mED|<1C|mAB|<1and|mED|>1D|mAB|>1and|mED|>1
The formula governing reflection of light from a spherical mirror is
1v+1u=2R, where
u = distance of object from pole of mirror,
υ = distance of image from pole of mirror
f = focal length of mirror,
R = radius of curvature of mirror.
This is known as mirror formula and is applicable equally to concave mirror and convex mirror.
m=IO=υu
Read the above passage and answer the following questions :
(i) An object is held at a distance of 30cm in front of a concave mirror of radius of curvature 40cm. Calculate distance of the image from the object ? What is linear magnification of the mirror ?
(ii) The object is moved to a distance of 40cm in front of the mirror. How is focal length of mirror affected ?
(iii) What values of life do you learn from the mirror formula ?
View SolutionA concave mirror has a radius of curvature of 24 cm. How far is an object from the mirror, if an image is formed that is
(i) virtual and 3.0 times the size of the object,
(ii) real and 3.0 times the size of the object and
(iii) real and 1/3 the size of the object?
View SolutionA concave mirror has a radius of curvature of 24 cm. How far is
an object from the mirror if an image is formed that is:
(a) virtual and 3.0 times the size of the object,
(b) real and 3.0 times the size of the object and
(c) real and 1/3 the size of the object?.
View SolutionA concave mirror is formed from a sphere of radius 20 cm. The image of an object at an infinite distance is formed at a distance of _____ cm from the mirror.
View SolutionA concave mirror is formed from a sphere of radius 20 cm. The image of an object at an infinite distance is formed at a distance of _____ cm from the mirror.
View SolutionFind the position of an object, which when placed in front of a concave mirror of radius of curvature 40 cm produces a virtual image, which is twice the size of the object.
View Solution

