Question

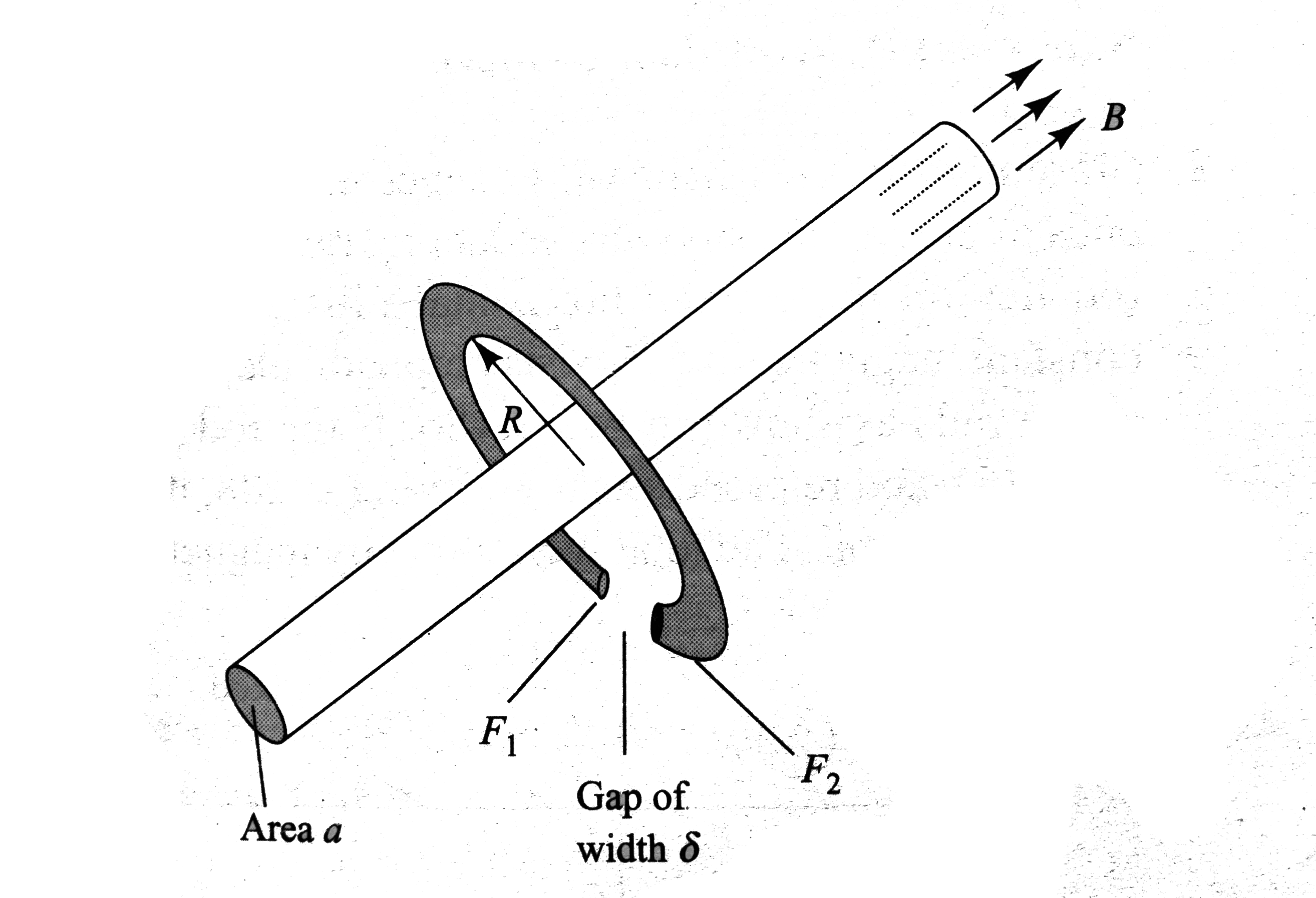
A highly conucting ring of radius $R$ is perpendicular to and concentric with the axis of a long solenoid as shown in fig. the ring has a narrow gap of width $d$ in its circumference. The solenoid has cross sectional area $A$ and a uniform internal field of magnitude $B_0$. Now beginning at $t=0$, the solenoid current is steadily increased to so that the field magnitude at any time $t$ is given by $B\left(t\right)=B_0+\alpha t$ where $\alpha >0$. Assuming that no charge can flow across the gap, the end of ring which has excess of positive charge and the magnitude of induced e.m.f. in the ring are respectively

Options

A. X, `Aalpha`
B. X, `piR^(2)alpha`
C. Y, `piA^(2)alpha`
D. Y, `piR^(2)alpha`

Answer

A

Explanation

`e=d/dt(BA)=Ad/dt(B_(0)+alphat)=Aalpha`
X `to` excess +ve charge because current flows in wing from Y to X (by Len.z law).