A long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
0.5
1.0 sec
0.25 sec
0.75 sec
The correct Answer is:C
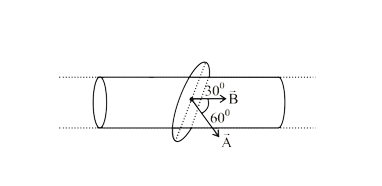
ϕB=BAcos60∘
=μ0nI0(t−2t2)A2
=μ0nI0A2(t−2t2)
For ϕB to be mmax
dϕBdt=0⇒1−4t=0⇒t=0.25sec.
Similar Questions
A wire carrying a current 15A and of length 4⋅0cm is placed inside a solenoid near its centre making an angle of 60∘ with the axis of solenoid, where the magnitude of the magnetic field due to the solenoid is 0⋅30T. What is the force on the wire?
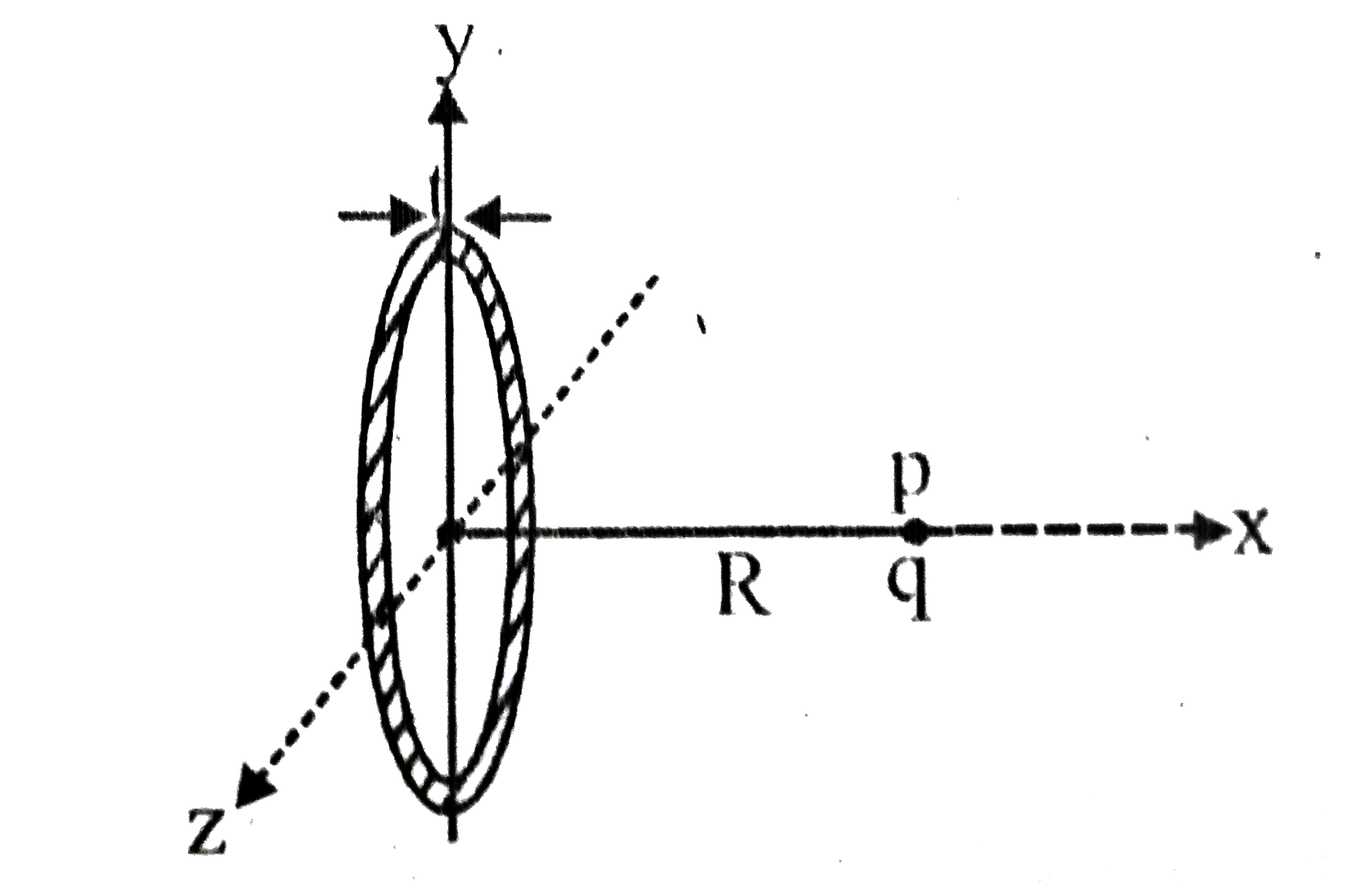
View SolutionA charge q is placed at the point P as shown in figure on the axis of the ring of elemental thickness 't' and radius R then flux through the ring is :-
View Solution
Knowledge Check
A long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
A0.5 secB1.0 secC0.25 secD0.75 secA long solenoid of radius R carries a time dependent current I=I0t(1–t). A ring of radius 2R is placed coaxially near its centre. During the time interval0≤t≤1, the induced current IR and the induced emf VR in the ring vary as:
Acurrent will change its direction and its emf will be zero at t = 0.25sec.Bcurrent will not change its direction & emf will be maximum at t = 0.5secCcurrent will not change direction and emf will be zero at 0.25sec.Dcurrent will change its direction and its emf will be zero at t = 0.5sec.A long solenoid of radius R carries a time (t)-dependent current I(t)=I0t2(1−t). A conducting ring of radius 3R is placed co-axially near its middle. During the time interva 0≤t≤1, the induced current (IR) in the ring varies as: [Take resistance of ring to be R0]
A B
B C
C D
D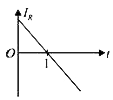
A circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
View Solutionlong solenoid of radius R carries a time –dependent current I(t)=I0(12t−t3) . A ring of radius 2R is placed coaxially near its middle. During the time interval 0≤t≤2√3 , the induced current (IR) and the induced EMF (VR) in the ring change as :
View SolutionA 0.100 m long solenoid has a radius of 0.050 m and 1.50×104 turns. The current in the solenoid changes at a rate of 6.0 A/s. A conducting loop of radius 0.0200 m is placed at the center of the solenoid with its axis the same as that of the solenoid as shown.
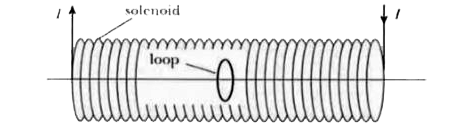
What is the magnetic flux through the small loop when the current through the solenoid is 2.50 A?
View SolutionA ring of area A and resistance R is placed on the axis of a solenoid. The mutual inductance between them is M. When the current in the solenoid changes at the rate of I, the magnetic moment of the ring is
View SolutionThe diagram given below shows a solenoid carrying time varying current l=l0t. On the axis of the solenoid, a ring has been placed. The mutual inductance of the ring and the solenoid is M and the self inductance of the ring is L. If the resistance of the ring is R then maximum current which can flow through the ring is
View Solution

