long solenoid of radius R carries a time –dependent current . A ring of radius 2R is placed coaxially near its middle. During the time interval , the induced current and the induced EMF in the ring change as :
At t = 1 direction of reverses and is maximum
At t = 2 direction of reverses and is zero
Direction of remain unchanged and is zero
Direction of remains unchanged and is maximum
The correct Answer is:B
in Ring .
Emf in Ring
I ve for
i ve for
So at t = 2 sec current through Ring reverses its direction.
And at t = 2EMF
Similar Questions
A coil A of radius R and number of turns n carries a current i and it is placed in a horizontal plane. A small conducting ring P of radius r(r<<R) is placed at a height y0 above the centre of the coil A as shown in figure-5.38. Calculate the induced EMF in the ring when the ring in allowed to fall freely. Express the induced EMF as a function of instantaneous speed of the falling ring and its height above the center of the coil A.

View SolutionThe current in a long solenoid of radius R and having n turns per unit length is given by i=i0sinωt. A coil having N turns is wound around it near the centre. Find (a) the induced emf in the coil and (b) the mutual inductance between the solenoid and the coil.
View Solution
Knowledge Check
A long solenoid of radius R carries a time dependent current I=I0t(1–t). A ring of radius 2R is placed coaxially near its centre. During the time interval0≤t≤1, the induced current IR and the induced emf VR in the ring vary as:
Acurrent will change its direction and its emf will be zero at t = 0.25sec.Bcurrent will not change its direction & emf will be maximum at t = 0.5secCcurrent will not change direction and emf will be zero at 0.25sec.Dcurrent will change its direction and its emf will be zero at t = 0.5sec.A long solenoid of radius R carries a time (t)-dependent current I(t)=I0t2(1−t). A conducting ring of radius 3R is placed co-axially near its middle. During the time interva 0≤t≤1, the induced current (IR) in the ring varies as: [Take resistance of ring to be R0]
A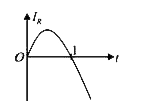 B
B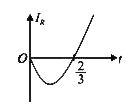 C
C D
D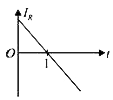
A long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
A0.5B1.0 secC0.25 secD0.75 sec
A long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
View SolutionA solenoid of radius R and length L has a current I=I0 cosωt. The value of induced electric field at a distance of r outside the solenoid, is
View SolutionA conducting ring of radius b is placed coaxially in a long solenoid of radius a (b < a) having n turns per unit length. A current i=i0, cosωt flows through the solenoid. The induced emf in the ring is
View SolutionIfS=2t3−4t2+12t, then distance travelled during the time -interval [0,1] is
View SolutionA solenoid of radius R number of turn per unit length n and length L has a current I=I0cosωt. The value of induced electric field at a distance of r outside the solenoid, is :
View Solution
