A long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
0.5
1.0 sec
0.25 sec
0.75 sec
The correct Answer is:C
To solve the problem, we need to determine the time at which the magnetic flux through the circular ring is maximum. The magnetic flux is directly related to the magnetic field produced by the solenoid, which in turn depends on the current flowing through it.
1. Identify the Current Function:
The current flowing through the solenoid is given by:
I(t)=I0(t−2t2)
2. Determine the Magnetic Field Inside the Solenoid:
The magnetic field B inside a long solenoid is given by:
B=μ0nI
where n is the number of turns per unit length and μ0 is the permeability of free space. Since n and μ0 are constants, we can express the magnetic field as:
B∝I(t)
3. Express the Magnetic Flux:
The magnetic flux Φ through the circular ring is given by:
Φ=B⋅A⋅cos(θ)
where A is the area of the ring and θ is the angle between the magnetic field and the normal to the plane of the ring. Given θ=30∘, we have:
Φ∝I(t)⋅A⋅cos(30∘)
4. Maximize the Current:
To find when the magnetic flux is maximum, we need to maximize the current I(t). We can do this by differentiating I(t) with respect to t and setting the derivative to zero:
dIdt=I0(1−4t)=0
Solving for t:
1−4t=0⟹t=14 seconds
5. Conclusion:
The time at which the magnetic flux through the ring is maximum is:
t=0.25 seconds
The current flowing through the solenoid is given by:
I(t)=I0(t−2t2)
The magnetic field B inside a long solenoid is given by:
B=μ0nI
where n is the number of turns per unit length and μ0 is the permeability of free space. Since n and μ0 are constants, we can express the magnetic field as:
B∝I(t)
The magnetic flux Φ through the circular ring is given by:
Φ=B⋅A⋅cos(θ)
where A is the area of the ring and θ is the angle between the magnetic field and the normal to the plane of the ring. Given θ=30∘, we have:
Φ∝I(t)⋅A⋅cos(30∘)
To find when the magnetic flux is maximum, we need to maximize the current I(t). We can do this by differentiating I(t) with respect to t and setting the derivative to zero:
dIdt=I0(1−4t)=0
Solving for t:
1−4t=0⟹t=14 seconds
The time at which the magnetic flux through the ring is maximum is:
t=0.25 seconds
Topper's Solved these Questions
Similar Questions
A long solenoid of radius R carries a time dependent current I=I0t(1–t). A ring of radius 2R is placed coaxially near its centre. During the time interval0≤t≤1, the induced current IR and the induced emf VR in the ring vary as:
View SolutionA long solenoid of radius R carries a time (t)-dependent current I(t)=I0t2(1−t). A conducting ring of radius 3R is placed co-axially near its middle. During the time interva 0≤t≤1, the induced current (IR) in the ring varies as: [Take resistance of ring to be R0]
View Solution
Knowledge Check
An 8 cm long wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. If the magnetic field inside the solenoid is 0.3 T, then magnetic force on the wire is
A0.14NB0.24NC0.34ND0.44N
long solenoid of radius R carries a time –dependent current I(t)=I0(12t−t3) . A ring of radius 2R is placed coaxially near its middle. During the time interval 0≤t≤2√3 , the induced current (IR) and the induced EMF (VR) in the ring change as :
View SolutionA very long solenoid of radius R is carrying current I(t)=kte−αt , as a function of time (t≥0). Counter clockwise current is taken to be positive. A circular conducting coil of radius 2R is placed in the equatorial plane of the solenoid and concentric with the solenoid. the current induced inthe outer coil is correctly depicted, as function of time by :
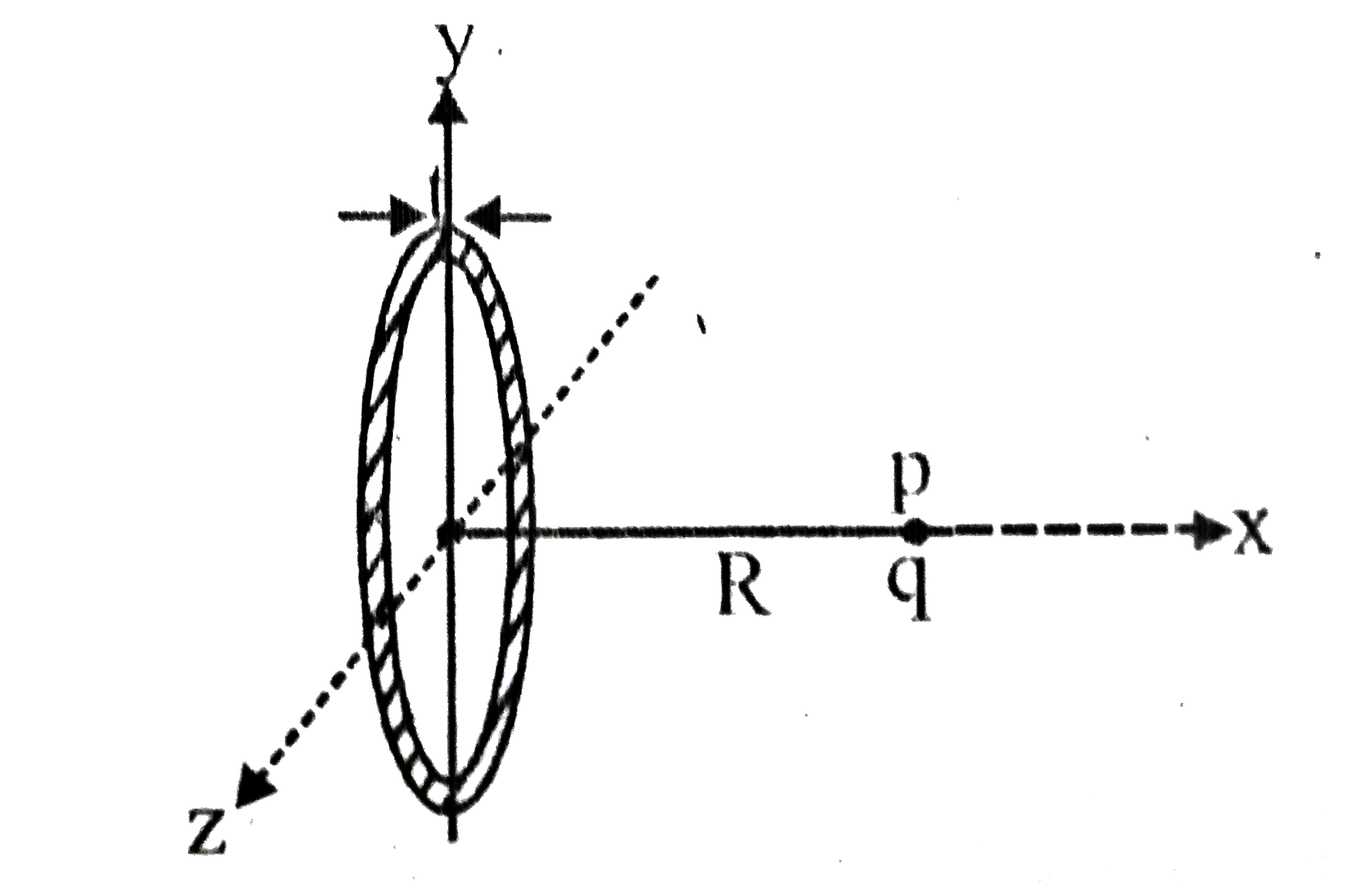
View SolutionA charge q is placed at the point P as shown in figure on the axis of the ring of elemental thickness 't' and radius R then flux through the ring is :-
View SolutionThe current in an ideal, long solenoid is varied at a uniform rate of 0.02A/s. The solenoid has 1000 turns/m and its radius is 8 cm.
(i) Consider a circle of radius 2 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 4 s.
(ii) Find the electric field induced at a point on the circumference of the circle.
(iii) Find the electric field induced at a point outside the solenoid at a distance 9 cm from its axis.
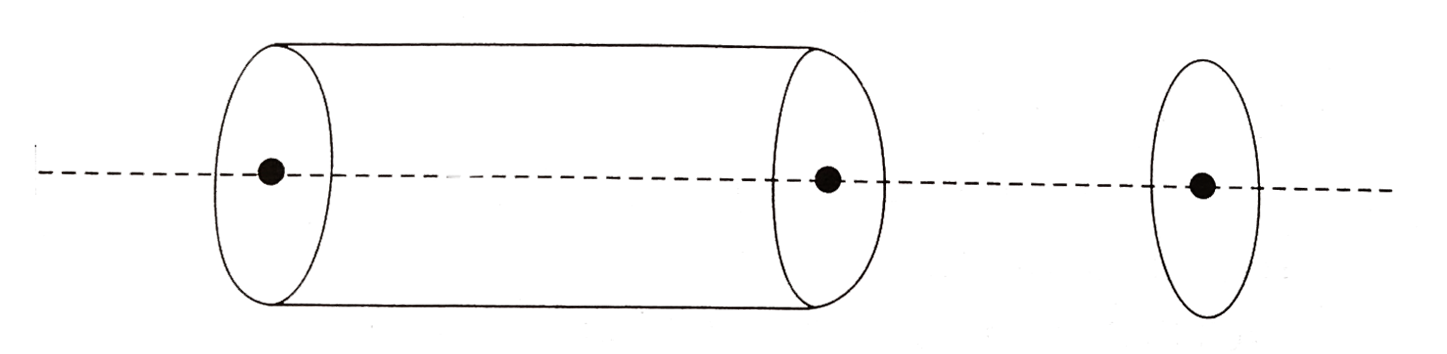
View SolutionThe diagram given below shows a solenoid carrying time varying current l=l0t. On the axis of the solenoid, a ring has been placed. The mutual inductance of the ring and the solenoid is M and the self inductance of the ring is L. If the resistance of the ring is R then maximum current which can flow through the ring is
View SolutionA circular loop of radius r carries a current i. where should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
View SolutionA 3⋅0cm wire carrying a current of 10A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0⋅27T. What is the magnetic force on the wire?
View Solution

