A long solenoid of radius R carries a time (t)-dependent current . A conducting ring of radius 3R is placed co-axially near its middle. During the time interva , the induced current in the ring varies as: [Take resistance of ring to be ]
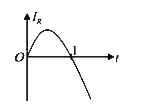
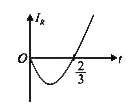

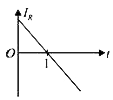
The correct Answer is:B
To solve the problem step by step, we will analyze the given information and apply relevant physics concepts.
Step 1: Understand the Current in the Solenoid
The current in the solenoid is given by:
I(t)=I0t2(1−t)
This indicates that the current varies with time.
Step 2: Calculate the Magnetic Field Inside the Solenoid
The magnetic field B inside a long solenoid is given by:
B=μ0nI
where n is the number of turns per unit length. Assuming the solenoid has n turns and using the given current:
B(t)=μ0nI0t2(1−t)
Step 3: Determine the Area of the Conducting Ring
The radius of the conducting ring is 3R. The area A of the ring is:
A=π(3R)2=9πR2
Step 4: Calculate the Magnetic Flux through the Ring
The magnetic flux Φ through the ring is given by:
Φ=B⋅A
Substituting the expressions for B and A:
Φ(t)=μ0nI0t2(1−t)⋅9πR2
Φ(t)=9μ0nI0πR2t2(1−t)
Step 5: Find the Induced EMF
According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−dΦdt
Differentiating Φ(t):
dΦdt=9μ0nI0πR2ddt(t2(1−t))
Using the product rule:
ddt(t2(1−t))=2t(1−t)−t2=2t−3t2
Thus,
E=−9μ0nI0πR2(2t−3t2)
Step 6: Calculate the Induced Current
The induced current IR in the ring can be calculated using Ohm's law:
IR=ER0
Substituting for E:
IR=−9μ0nI0πR2(2t−3t2)R0
Step 7: Determine When the Induced Current is Zero
To find when the induced current is zero, set the expression 2t−3t2=0:
t(2−3t)=0
This gives:
1. t=0
2. t=23
Conclusion
The induced current varies as a function of time and is zero at t=0 and t=23. The nature of the function IR indicates it is a quadratic function of time, which opens downwards (as indicated by the negative coefficient of t2).
The current in the solenoid is given by:
I(t)=I0t2(1−t)
This indicates that the current varies with time.
The magnetic field B inside a long solenoid is given by:
B=μ0nI
where n is the number of turns per unit length. Assuming the solenoid has n turns and using the given current:
B(t)=μ0nI0t2(1−t)
The radius of the conducting ring is 3R. The area A of the ring is:
A=π(3R)2=9πR2
The magnetic flux Φ through the ring is given by:
Φ=B⋅A
Substituting the expressions for B and A:
Φ(t)=μ0nI0t2(1−t)⋅9πR2
Φ(t)=9μ0nI0πR2t2(1−t)
According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−dΦdt
Differentiating Φ(t):
dΦdt=9μ0nI0πR2ddt(t2(1−t))
Using the product rule:
ddt(t2(1−t))=2t(1−t)−t2=2t−3t2
Thus,
E=−9μ0nI0πR2(2t−3t2)
The induced current IR in the ring can be calculated using Ohm's law:
IR=ER0
Substituting for E:
IR=−9μ0nI0πR2(2t−3t2)R0
To find when the induced current is zero, set the expression 2t−3t2=0:
t(2−3t)=0
This gives:
1. t=0
2. t=23
The induced current varies as a function of time and is zero at t=0 and t=23. The nature of the function IR indicates it is a quadratic function of time, which opens downwards (as indicated by the negative coefficient of t2).
Topper's Solved these Questions
Similar Questions
A long solenoid of radius R carries a time dependent current I=I0t(1–t). A ring of radius 2R is placed coaxially near its centre. During the time interval0≤t≤1, the induced current IR and the induced emf VR in the ring vary as:
View Solutionlong solenoid of radius R carries a time –dependent current I(t)=I0(12t−t3) . A ring of radius 2R is placed coaxially near its middle. During the time interval 0≤t≤2√3 , the induced current (IR) and the induced EMF (VR) in the ring change as :
View SolutionA long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
View SolutionA long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
View SolutionA conducting ring of radius b is placed coaxially in a long solenoid of radius a (b < a) having n turns per unit length. A current i=i0, cosωt flows through the solenoid. The induced emf in the ring is
View SolutionSwitch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
View SolutionThe diagram shows a solenoid carrying time varying current I=I0t (I0 is constant) on the axis of this solenoid a conducting ring is being placed as shown in the figure. The mutual inductance of the ring and the solenoid is M and self inductance of the ring is L . if the resistance of the ring is R then the maximum current which can flow through the ring is
View SolutionIf i=t2,0<t<T then r.m.s. value of current is
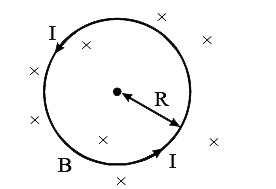
View SolutionA current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
View SolutionA very long solenoid of radius R is carrying current I(t)=kte−αt , as a function of time (t≥0). Counter clockwise current is taken to be positive. A circular conducting coil of radius 2R is placed in the equatorial plane of the solenoid and concentric with the solenoid. the current induced inthe outer coil is correctly depicted, as function of time by :
View Solution
