A container of height 10 m which is open at the top. has water to its full height. Two small openings are made on the walls of the container one exactly at the middle and the other at the bottom. The ratio of the velocities with which water comes out from the middle and the bottom region respectively is
2
12
√2
1√2
The correct Answer is:D
To solve the problem, we need to determine the ratio of the velocities of water exiting from two openings in a container filled with water. One opening is located at the middle of the container, and the other is at the bottom.
1. Identify the heights of the openings:
- The total height of the container is given as h=10m.
- The height of the opening at the middle of the container is h1=h2=102=5m.
- The height of the opening at the bottom of the container is h2=h=10m.
2. Use Torricelli's Law:
- According to Torricelli's Law, the velocity of fluid flowing out of an opening under the influence of gravity is given by the formula:
v=√2gh
- Here, g is the acceleration due to gravity, and h is the height of the fluid above the opening.
3. Calculate the velocities:
- For the opening at the middle (height h1):
v1=√2gh1=√2g⋅5=√10g
- For the opening at the bottom (height h2):
v2=√2gh2=√2g⋅10=√20g
4. Find the ratio of the velocities:
- The ratio of the velocities v1v2 is given by:
v1v2=√10g√20g=√10√20=√10√10⋅2=1√2
5. Final Result:
- Therefore, the ratio of the velocities with which water comes out from the middle and the bottom openings is:
v1v2=1√2
- The total height of the container is given as h=10m.
- The height of the opening at the middle of the container is h1=h2=102=5m.
- The height of the opening at the bottom of the container is h2=h=10m.
- According to Torricelli's Law, the velocity of fluid flowing out of an opening under the influence of gravity is given by the formula:
v=√2gh
- Here, g is the acceleration due to gravity, and h is the height of the fluid above the opening.
- For the opening at the middle (height h1):
v1=√2gh1=√2g⋅5=√10g
- For the opening at the bottom (height h2):
v2=√2gh2=√2g⋅10=√20g
- The ratio of the velocities v1v2 is given by:
v1v2=√10g√20g=√10√20=√10√10⋅2=1√2
- Therefore, the ratio of the velocities with which water comes out from the middle and the bottom openings is:
v1v2=1√2
Topper's Solved these Questions
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - PAST YEARS QUESTIONS
14 Videos
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - ASSERTION AND REASON
23 Videos
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - NCERT BASED QUESTIONS(PASCAL.S LAW AND ARCHIMEDES PRINCIPLE)
23 Videos
- ELASTICITYBOOK - ERRORLESSCHAPTER - ELASTICITYEXERCISE - ASSERTION & REASON
10 Videos
- FRICTION BOOK - ERRORLESSCHAPTER - FRICTION EXERCISE - ASSERTION & REASON
8 Videos
Similar Questions
A cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure =1.0×105N/m2, density of water=1000kg//m^3andg=10m//s^2. Neglect any effect of surface tension.]
View SolutionA cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure =1.0×105N/m2, density of water=1000kg//m^3andg=10m//s^2. Neglect any effect of surface tension.]
View Solution
Knowledge Check
In a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
Aproportional to hBproportional to h1/2Cproportional to h2Dindependent of hA tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :
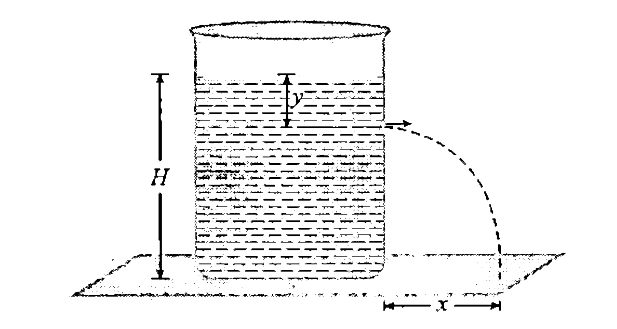 AIF y is increased from zero to H, x will first increase and then decreaseBx is maximum for y=H/2CThe maximum value of x is HDThe maximum value of x will depend on the density of the liquid
AIF y is increased from zero to H, x will first increase and then decreaseBx is maximum for y=H/2CThe maximum value of x is HDThe maximum value of x will depend on the density of the liquidA hole is made in the bottom of a container having water filled up to a height h. The velocity of water flowing out of the hole is :
Aindependent of h .Bproportional to h1/2Cproportional to hDproportional to h2
Water is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
View SolutionA tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :

View SolutionA cylinder of height 20m is completely filled with water. The velocity of effux of water (∈ms−1) through a small hole on the side wall of the cylinder near its bottom is
View SolutionA cylinder of height 20 m is completely filled with water. The velocity of efflux of water through a hole on the side wall of the cylinder near its bottom is (Take g=10ms−2)
View SolutionThe pressure of water in a pipe when tap is closed is 5.5×105Nm−2. The velocity with which water comes out on opening the tap is
View Solution
