Water flows steadily through a horizontal pipe of a variable cross-section. If the pressure of water is p at a point where the velocity of flow is v, what is the pressure at another point where the velocity of flow is 2v, $ρ$ being the density of water?

A

$P - \frac{3 ρ v^{2}}{2}$

B

$P - \frac{ρ v^{2}}{2}$

C

$P - \frac{3 ρ v^{2}}{4}$

D

$P - ρ v^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

According to Bernoulli.s principle -
$P + \frac{1}{2} ρ v^{2}$ = Constant
$\Rightarrow P + \frac{1}{2} ρ v^{2} = P . + \frac{1}{2} ρ {(2 v)}^{2}$
$\Rightarrow P . = P - \frac{3}{2} ρ v^{2}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Water flows steadily through a horizontal pipe of a variable cross-section. If the pressure of the water is p at a point , where the speed of the flow is v. What is the pressure at another point , where the speed of the flow is 2 v ? Let the density of water be $1 g c m^{- 3}$ .
A $p + (\frac{3}{2}) ρ v^{2}$
B $p - 2 ρ v^{2}$
C $p - 3 ρ v^{2}$
D $p - (\frac{3}{2}) ρ v^{2}$
Question 2 - Select One
Water flows steadily through a horizontal pipe of variable cross-section. If the pressure of water is $p$ at a point where the velocity of flow is $v$ , at another point (pressure $p'$ ), where the velocity of flow in $η v$ : The following statements are given below
A $\frac{p'}{p} < 1$ , when $η < 1$
B $\frac{p'}{p} < 1$ , when $η > 1$
C $\frac{p'}{p} > 1$ , when $η < 1$
D $\frac{p'}{p} > 1$ , when $η > 1$
Question 3 - Select One
Water is flowing steadily through a horizontal pipe of non-uniform cross-section. If the pressure of water is $4 \times 10^{4} N / m^{2}$ at a point where cross-section is $0.02 m^{2}$ and velocity of flow is $2 m / s$ . What is the pressure at a point where cross-section reduces to $0.01 m^{2}$ ?
.
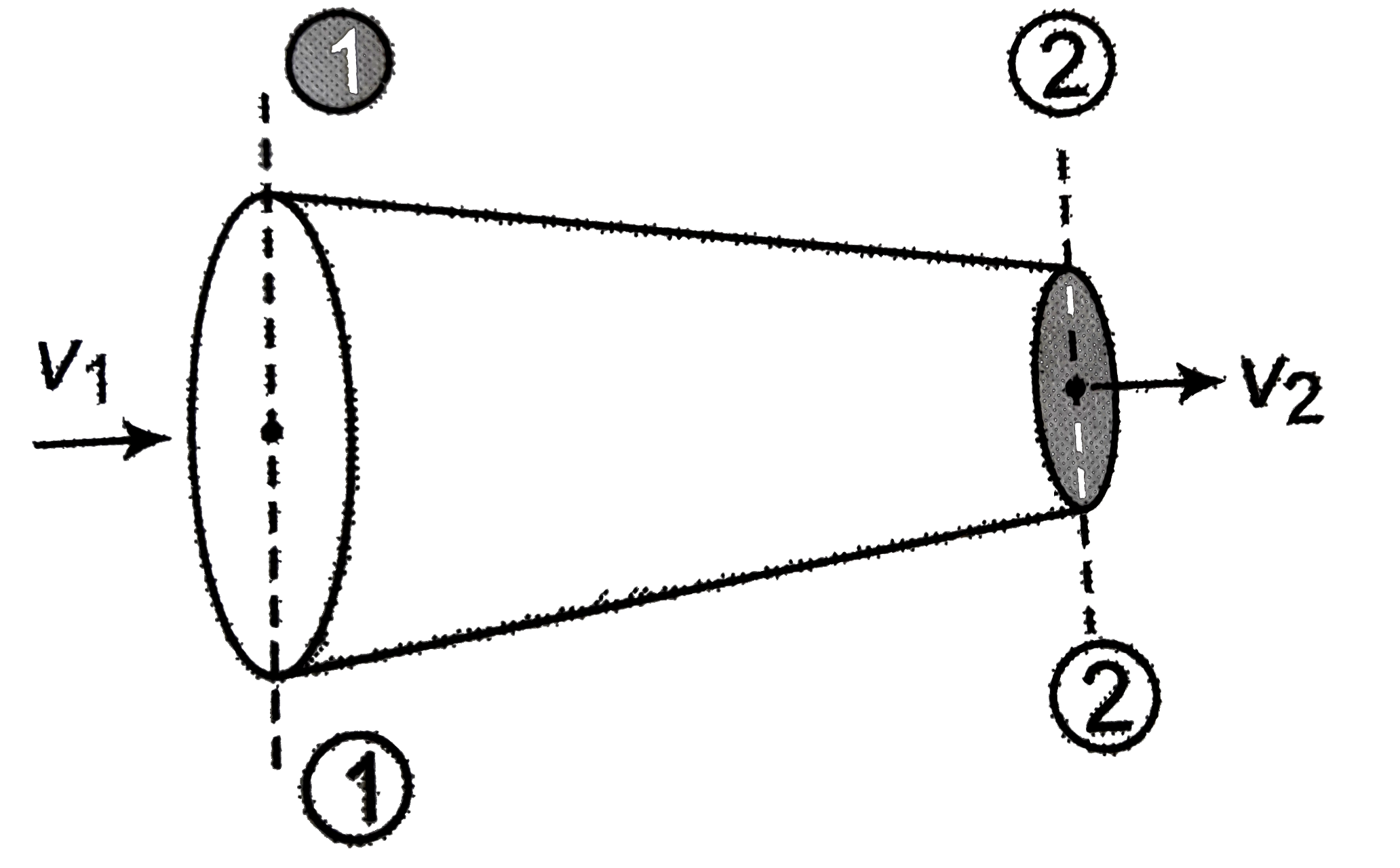A $1.4 \times 10^{4} N / m^{2}$
B $3.4 \times 10^{4} N / m^{2}$
C $2.4 \times 10^{- 4} N / m^{2}$
Dnone of these

ERRORLESS-FLUID MECHANICS-NCERT BASED QUESTIONS(FLUID FLOW)

Home
Ask Doubt
Profile