A sniper fires a rifle bullet into a gasoline tank making a hole below the surface of gasoline. The tank was sealed at 3.10 atm . The stored gasoline has a density of . The velocity with which gasoline begins to shoot out of the hole is
27.8m
41.0m
9.6m
19.7 m
The correct Answer is:B
According to Bernoulli.s principle -
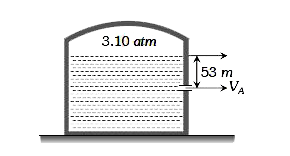
.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - PAST YEARS QUESTIONS
14 Videos
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - ASSERTION AND REASON
23 Videos
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - NCERT BASED QUESTIONS(PASCAL.S LAW AND ARCHIMEDES PRINCIPLE)
23 Videos
- ELASTICITYBOOK - ERRORLESSCHAPTER - ELASTICITYEXERCISE - ASSERTION & REASON
10 Videos
- FRICTION BOOK - ERRORLESSCHAPTER - FRICTION EXERCISE - ASSERTION & REASON
8 Videos
Similar Questions
A tank containing gasoline is sealed and the gasoline is under pressure P0 as shown in the figure. The stored gasoline hs a density of 660kgm−3. A sniper fires a rifle bullet into the gasoline tank, making a small hole 53m below the surface of gasoline. The total height of gasoline is 73m from the base. The jet of gasoline shooting out of the hole strikes the ground at a distance of 80m from the tank initially. If the pressure above the gasonline surface is (1.39)α×105N/m2 than α is- (The local atmospheric pressure is 105Nm−2)
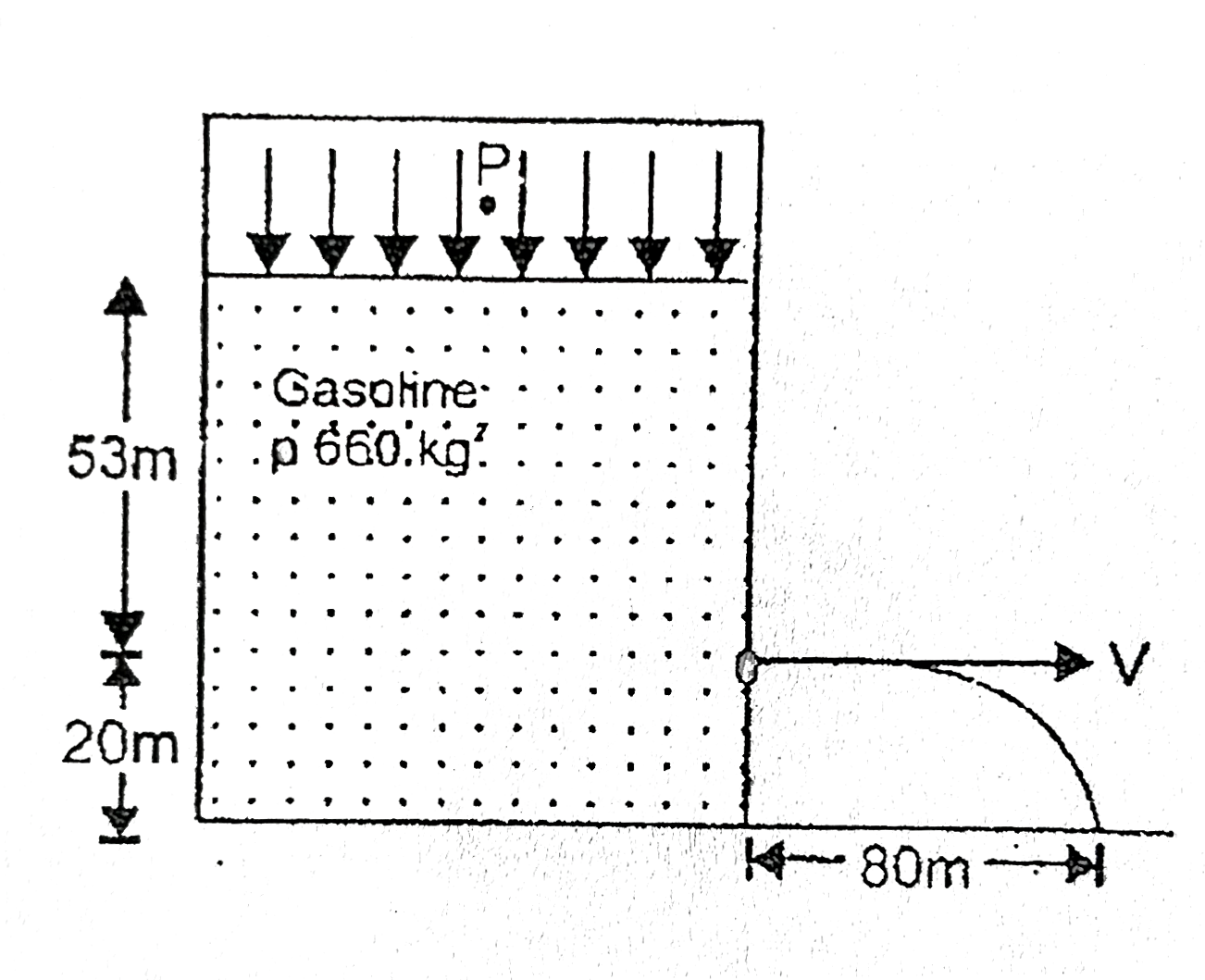
View SolutionA hollow sphere has a small hole in it. On lowering the sphere in a tank of water, it is observed that water enters into the hollow sphere at a depth of 40cm below the surface. Surface tension of water is 7×10−2N/m. The diameter of the hole is
View Solution
Knowledge Check
A water tank, open to the atmosphere, has a leak in it in the form of a circular hole, located at a height h below the open surface of water. The velocity of the water coming out of the hole is :
A√gh/2B√ghC√2ghD2√ghA water tank, open to the atmosphere, has a leak in it in the form of a circular hole, located at a height h below the open surface of water. The velocity of the water coming out of the hole is :
A√gh/2B√ghC√2ghD2√ghThe piston is taken completely out of the cylinder. The hole at the top is sealed. A water tank is brough below the cylinder and put in a positoon so that the water surface in the tank is at the same level as the top of the cylinder as shown in the fgure. The density of the water is rho.In equilibriium, the height H of the water column in the cylinder satisfies
 Aρg(L0−H)2+P0(L0−H)+(L0P0)=0Bρg(L0−H)2−P0(L0−H)−L0P0=0Cρg(L0−H)2+P0(L0−H)−L0P0=0Dρ(L0−H)2−P0(L0−H)+(L0P0)=0
Aρg(L0−H)2+P0(L0−H)+(L0P0)=0Bρg(L0−H)2−P0(L0−H)−L0P0=0Cρg(L0−H)2+P0(L0−H)−L0P0=0Dρ(L0−H)2−P0(L0−H)+(L0P0)=0
A fixed thermally conducting cylinder has a radius R and height L0. The cylinder is open at ita bottom and has a small hole at its top. A piston of mass M is held at a distance L from the top surface, as shown in the figure. The atmospheric pressure is P0.
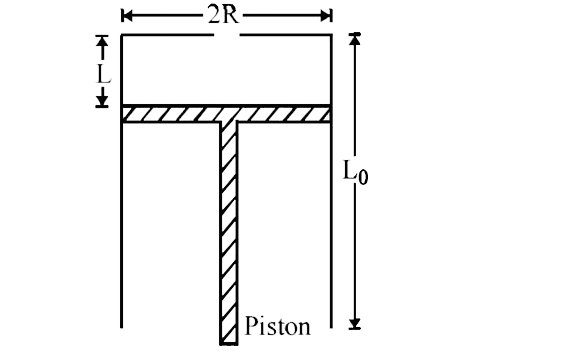
The piston is taken completely out of the cylinder. The hole at the top is sealed. A water tank is brought below the cylinder and put in a position so that the water surface in the tank is at the same level as the top of the cylinder as shown in the figure. The density of the water is ρ. In equilibrium, the height H of the water coulmn in the cylinder satisfies

View SolutionA hollow sphere has a small hole in it. On lowering the sphere in a tank of water, it is observed that water enters into the hollow sphere at a depth of 40 cm below the surface. Surface tension of water is 7×10−2N/m. The diameter of the hole is approximately :
View SolutionA cylindrical tank is filled with water to a level of 4 m. A hole is opened at a height of 60 cm from bottom. The ratio of the area of the hole to that at cross-sectinal area at cylinder is 0.2. Then the velocity with which water is coming out is (g=10m/s2)
View SolutionA cylindrical tank is filled with water to a level of 3m. A hole is opened at a height of 52.5 cm from bottom. The ratio of the area of the hole to that of cross-sectional area of the cylinder is 0.1. The square of the speed with which water is coming out from the orifice is (Take g=10m/s2)
View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height h0 and pressure 2p0 where rh0 is the atmospheric pressure. There is a hole in the wall of the tank at a depth h1 below the top from which water comes out. A long vertical tube is connected as shown.

Find the height of the water in the long tube above the top when the water stops coming out of the hole.
View Solution
