A block off mass 200 g executing SHM under the unfluence of a spring of spring constant k=90Nm−1 and a damping constant gb=40gs−1. The time elaspsed for its amplitude to drop to halff of its initial value is (Given, ln (1/2)=−0.693)
7s
9s
4s
11s
The correct Answer is:A
Amplitude of damped oscillator-
A(t)=A0e−bt/2m
⇒A02=A0e−bt2m⇒ln(12)=−bt2m
⇒−0.693=−40×10−3×t2×0.2
⇒t=2×0.2×0.69340×10−3=6.93 sec
⇒t≈7 sec.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - NCERT BASED QUESTIONS (Superposition of S.H.M.s and Resonance)
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - PAST YEARS QUESTIONS
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - NCERT BASED QUESTIONS (Simple Pendulum)
27 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - Assertion & Reason
25 Videos
- SURFACE TENSIONBOOK - ERRORLESSCHAPTER - SURFACE TENSIONEXERCISE - ASSERTION & REASON
11 Videos
Similar Questions
In damped oscillatory motion a block of mass 20kg is suspended to a spring of force constant 90N/m in a medium and damping constant is 40g/s. Find (a) time period of oscillation (b) time taken for amplitude of oscillation to drop to half of its intial value (c) time taken for its mechanical energy to drop to half of its initial value.
View SolutionAmplitude of mass spring system which is executing SHM decreases with time. If mass = 500g decay constant = 20 g/s then how much time is required for the amplitude of the system to drop to half of its initial value.
View Solution
Knowledge Check
A block of mass 0.1 kg is connected to an elastic spring of spring constant 640 Nm−1 and oscillates in a medium of constant 10−2 kg s−1. The system dissipates its energy gradually. The time taken for its mechanical energy of vibration to drop to half of its initial value, is closest to :
A2 sB3.5 sC5 sD7 sFor the small damping oscillator, the mass of the block is 500 g and value of spring constant is k = 50 N/m and damping constant is 10 g s^(-1) The time period of oscillation is (approx.)
A2πsB2π13sCπ5sDπ√5sA block of mass 2kg is propped from a height of 40cm on a spring where force constant is 1960Nm−1 The maximum distance thought which the spring compressed by
A5cmB15cmC26cmD10cm
For the damped oscillator shown in Fig, the mass of the block is 200g,k=80Nm−1 and the damping constant b is 40gs−1 Calculate
(a) The period of oscillation
(b) Time taken for its amplitude of vibrations to drop to half of its initial values
(c) The time for the mechanical energy to drop to half initial values
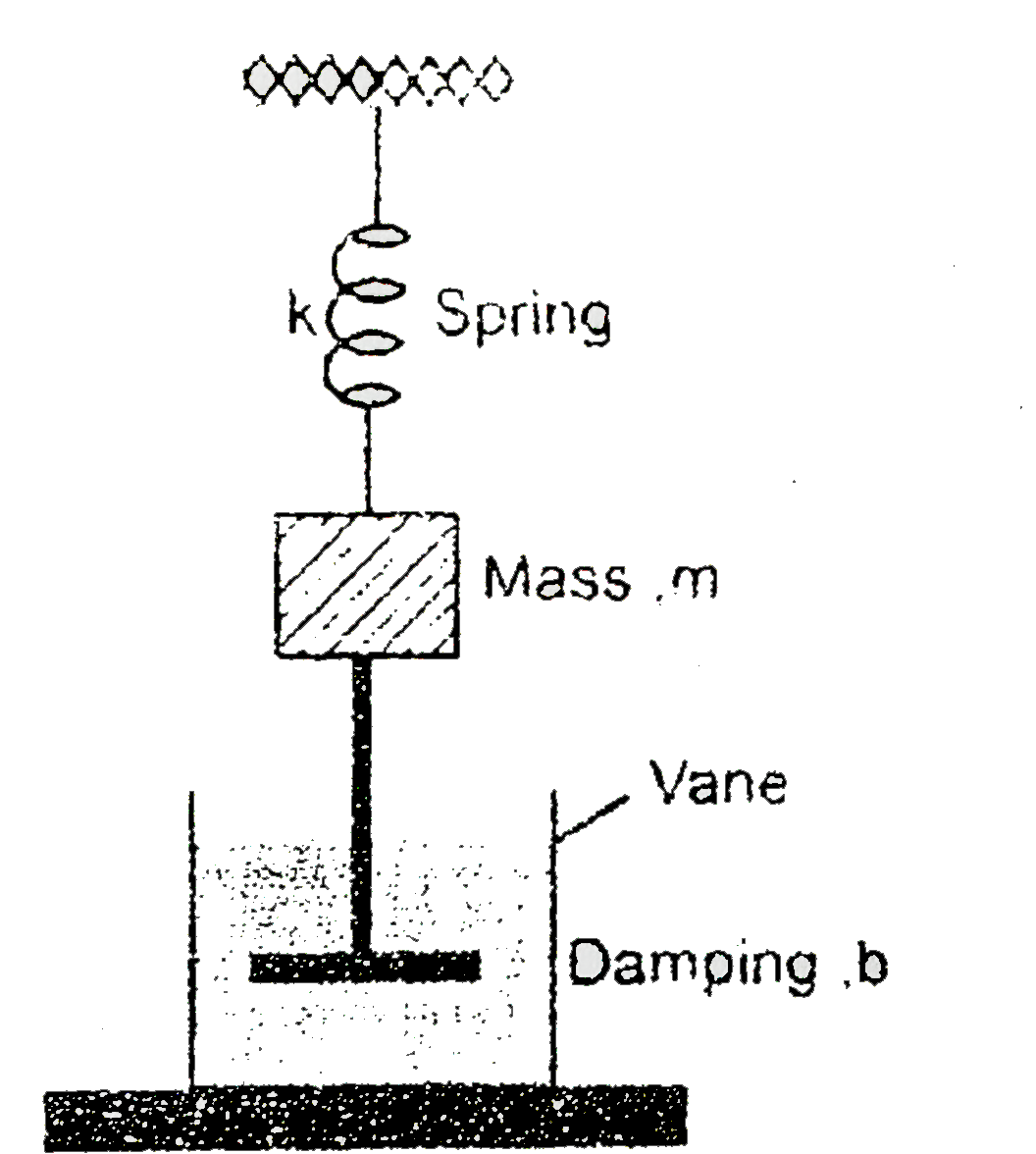
View SolutionAmplitude of a mass-spring system, which is executing simple harmonic motion decreases with time. If mass=500g, Decay constant=20 g/s then how much time is required for the amplitude of the system to drop to half of its initial value ? (In 2=0.693)
View SolutionFor the damped oscillator shown in previous Figure, the mass m of the block is 400 g, k=45Nm−1 and the damping constant b is 80gs−1. Calculate .
(a) The period of osciallation ,
(b) Time taken for its amplitude of vibrations to drop to half of its initial value and
(c ) The time taken for its mechanical energy to drop to half its initial value.
View SolutionBy what fraction does the mass of a spring is 200 g at its natural lenth and the spring constant is 500 N m ^(-1)
View SolutionFor a damped oscillator the mass 'm' of the block is 200 g, k = 90 N m−1 and the damping constant b is 40 g s−1. Calculate the period of oscillation.
View Solution
