A particle of mass $m$ is under the influence of a force F which varies with the displacement x according to the relation $F = - k x + F_{0}$ in which k and $F_{0}$ are constants. The particle when disturbed will oscillate

about x=0, with $w \neq \sqrt{k / m}$

about x=0, with $ω = \sqrt{k / m}$

about $x = F_{0} / k$ with $ω = \sqrt{k / m}$

about $x = F_{0} / k$ with $ω \neq \sqrt{k / m}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

A particle of mass M originally at rest is subjected to a force whose direction is constant but magnitude varies with time according to the relation
$F = F_{0} [1 - {(\frac{t - T}{T})}^{2}]$
Where $F_{0}$ and T are constants. The force acts only for the time interval 2T. The velocity v of the particle after time 2T is :
A $2 F_{0} T / M$
B $F_{0} T / 2M$
C $4 F_{0} T / 3M$
D $F_{0} T / 3M$
A particle of mass $1 k g$ moves from rest along a straight line due to acition of a force $F$ which varies with the displacement $x$ as shown in graph $- ($ Use $\frac{1}{\sqrt{2}} = 0.8$ if needed $)$

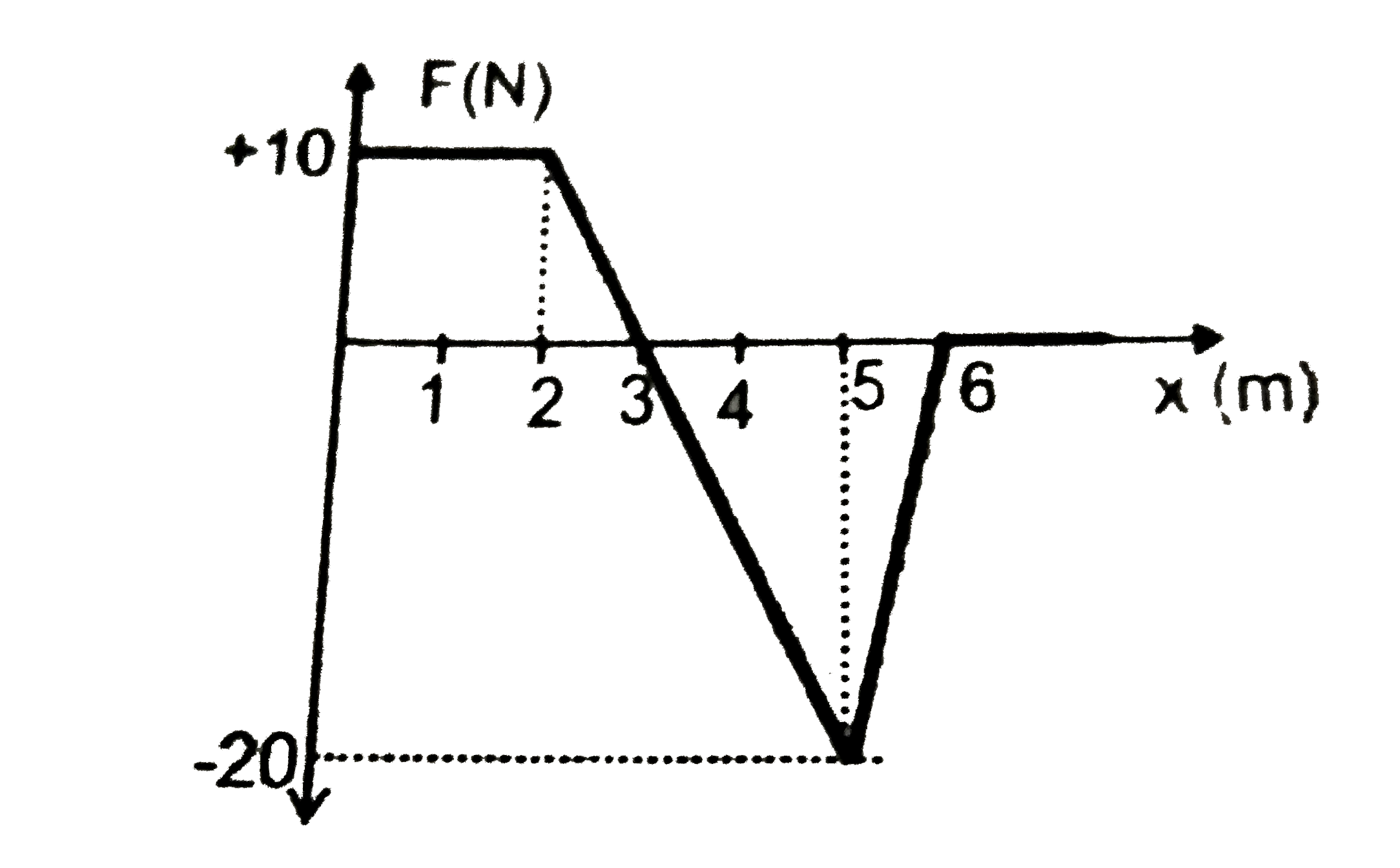Amaximum $K . E .$ of particle is $25 J$
BTotal work done by froce on particle up to $x = 6 m$ is $- 5 J$
CThere will beno power delivered by the particle at $x = 3, 5.3$ and $6 m$
DNone of these
A particle of mass m is acted upon by a force $F = t^{2} - k x$ . Initially , the particle is at rest at the origin. Then
Aits displacement will be in simple harmonic
Bits velocity will be in simple harmonic
Cits acceleration will be in simple harmonic
DNone of the above