A particle is moving along x-axis under the action of force, F which varies with its position as F∝14√x. Find the variation of power due to this fore with x.
To solve the problem, we need to find the variation of power due to a force F that varies with position x as F∝14√x. We will follow these steps:
Step 1: Express the Force
Given that F∝14√x, we can express this as:
F=k⋅14√x=k4x−1/2
where k is a proportionality constant.
Step 2: Relate Force to Acceleration
From Newton's second law, we know that:
F=ma
This implies:
ma=k4x−1/2
Thus, the acceleration a can be expressed as:
a=Fm=k4mx−1/2
Step 3: Relate Acceleration to Velocity
Acceleration a is the rate of change of velocity v with respect to time t:
a=dvdt
We can also express acceleration in terms of position x as:
a=dvdx⋅dxdt=vdvdx
Setting the two expressions for acceleration equal gives us:
vdvdx=k4mx−1/2
Step 4: Separate Variables and Integrate
We can separate variables and integrate:
vdv=k4mx−1/2dx
Integrating both sides:
∫vdv=∫k4mx−1/2dx
This results in:
v22=k4m⋅2x1/2+C
v2=k2mx1/2+C′
Step 5: Find the Relationship Between Velocity and Position
Assuming C′=0 for simplicity, we have:
v2∝x1/2
Thus,
v∝x1/4
Step 6: Calculate Power
Power P is given by the product of force and velocity:
P=F⋅v
Substituting our expressions for F and v:
P∝(k4x−1/2)⋅(x1/4)
This simplifies to:
P∝k4x−1/2⋅x1/4=k4x−1/2+1/4=k4x−1/4
Step 7: Final Expression for Power
Thus, we find:
P∝x−1/4
Summary
The variation of power due to the force with respect to x is given by:
P∝x−1/4
Given that F∝14√x, we can express this as:
F=k⋅14√x=k4x−1/2
where k is a proportionality constant.
From Newton's second law, we know that:
F=ma
This implies:
ma=k4x−1/2
Thus, the acceleration a can be expressed as:
a=Fm=k4mx−1/2
Acceleration a is the rate of change of velocity v with respect to time t:
a=dvdt
We can also express acceleration in terms of position x as:
a=dvdx⋅dxdt=vdvdx
Setting the two expressions for acceleration equal gives us:
vdvdx=k4mx−1/2
We can separate variables and integrate:
vdv=k4mx−1/2dx
Integrating both sides:
∫vdv=∫k4mx−1/2dx
This results in:
v22=k4m⋅2x1/2+C
v2=k2mx1/2+C′
Assuming C′=0 for simplicity, we have:
v2∝x1/2
Thus,
v∝x1/4
Power P is given by the product of force and velocity:
P=F⋅v
Substituting our expressions for F and v:
P∝(k4x−1/2)⋅(x1/4)
This simplifies to:
P∝k4x−1/2⋅x1/4=k4x−1/2+1/4=k4x−1/4
Thus, we find:
P∝x−1/4
The variation of power due to the force with respect to x is given by:
P∝x−1/4
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:IILUSTRATION
Explore 2 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:TRY YOURSELF
Explore 95 Videos
- WAVESBook:AAKASH INSTITUTEChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
A particle is moving along x-axis under the action of a force F, which varies with its position (x)asf∝1√x.Find the variation of power due to this force with x.
View SolutionForce acting on a particle varies with the distance travelled by the particle as F prop(1)/((x)^(1/3)) then power due to this force varies with as:
View Solution
Knowledge Check
A particle is moving along x-axis under the action of a force, F which varies with its position (x) as F∝x−1/4. The variation of power due to this force with x is
Ax1/3Bx1/8Cx1/2Dt1/4A particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (1):Ait is moving along negative X-direction with a speed that is increasing with timeBit is moving along positive X-direction with a speed that is decreasing with timeCit is moving along negative X-direction with a speed that is decreasing with timeDit is moving along positive X-direction with a speed that is increasing with timeA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (3) :Ait is moving along positive X-direction with a maximum speedBit is moving along negative X-direction with a speed that is increasing with timeCit is moving along positive X-direction with a speed that is decreasing with timeDit is moving along negative X-direction with a speed that is decreasing with time
A particle is moving along X-axis under a force such that its position -time graph is as shown in figure.
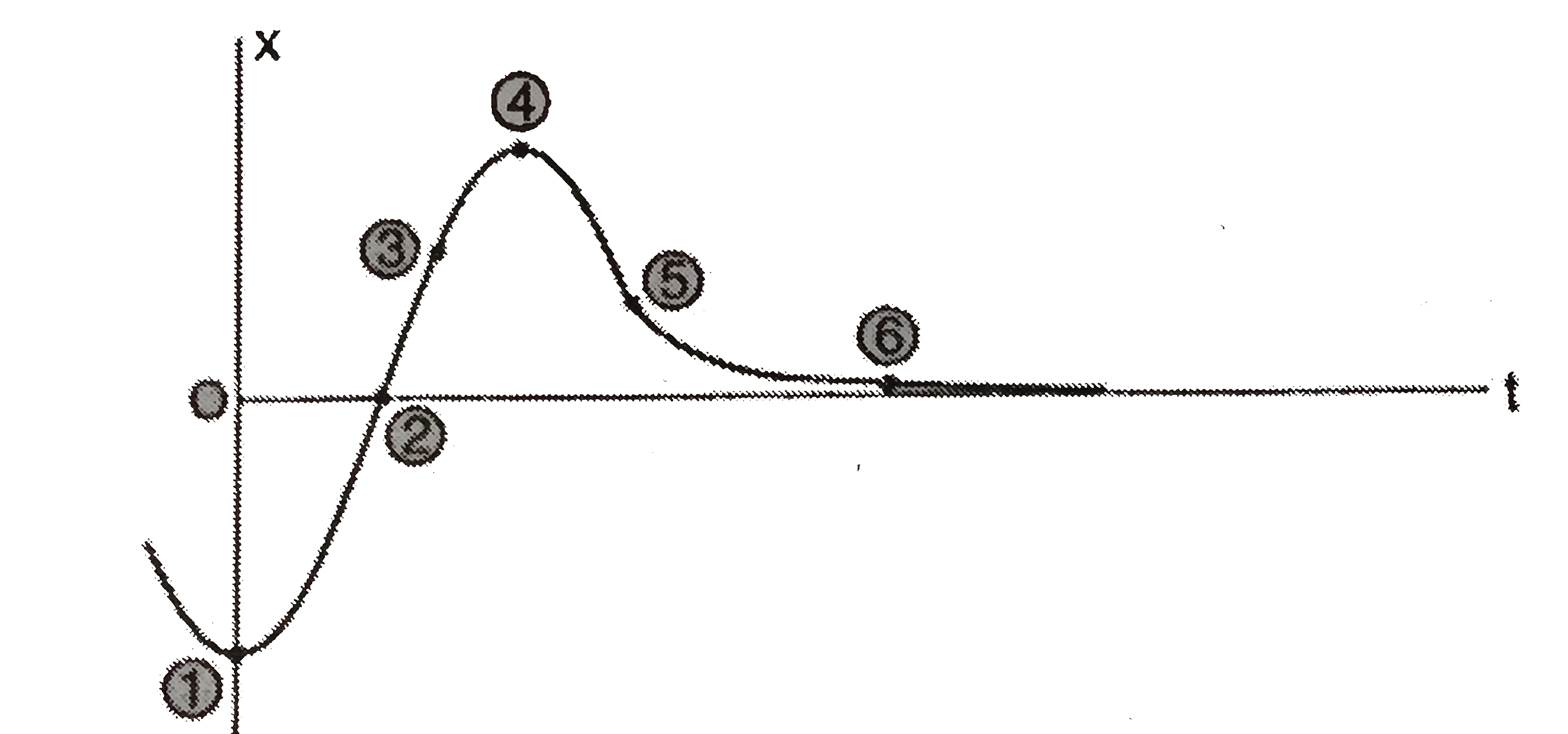
As the particle passes position (6) :
View SolutionA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (2):
View SolutionA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (5) :
View SolutionA particle starts moving from rest along y axis and a variable force F acts on it such that F∞y−15 (y>0). The variation of power P of this force with y is given as
View SolutionA particle is moving along x-axis. Its velocity v with x co-ordinate is varying as v=√x. Then
View Solution
