A particle is moving along -axis. Its velocity with co-ordinate is varying as . Then
initial velocity of particle is zero
motion is non-uniformly accelerated
acceleration of particle at is
acceleration of particle at is
The correct Answer is:A, C
Step by step video, text & image solution for A particle is moving along x-axis. Its velocity v with x co-ordinate is varying as v=sqrt(x). Then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:COMPREHENSION_TYPE
Explore 19 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:MATCH THE COLUMN
Explore 10 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 11 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Medical entrances gallery
Explore 39 Videos
Similar Questions
A particle is moving along x-axis such that its velocity varies with time according to v=(3m/s2)t−(2m/s3)t2. Find the velocity at t = 1 s and average velocity of the particle for the interval t = 0 to t = 5 s.
View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View Solution
Knowledge Check
Consider a particle moving along x-axis. Its distance from origin O is described by the co-ordinate x which varies with time. At a time t1, the particle is at point P, where its co-ordinate is x1 and at time t2, the particle is at point Q, where its co-ordinate is x2. The displacement during the time interval from t1 to t2 is the vector from P to Q, the x-component of this vector is (x2−x1) and all other components are zero.
It is convenient to represent the quantity x2−x1 the change in x by means of a notation Δ, thus Δx=x2−x1 and Δt=t2−t1.
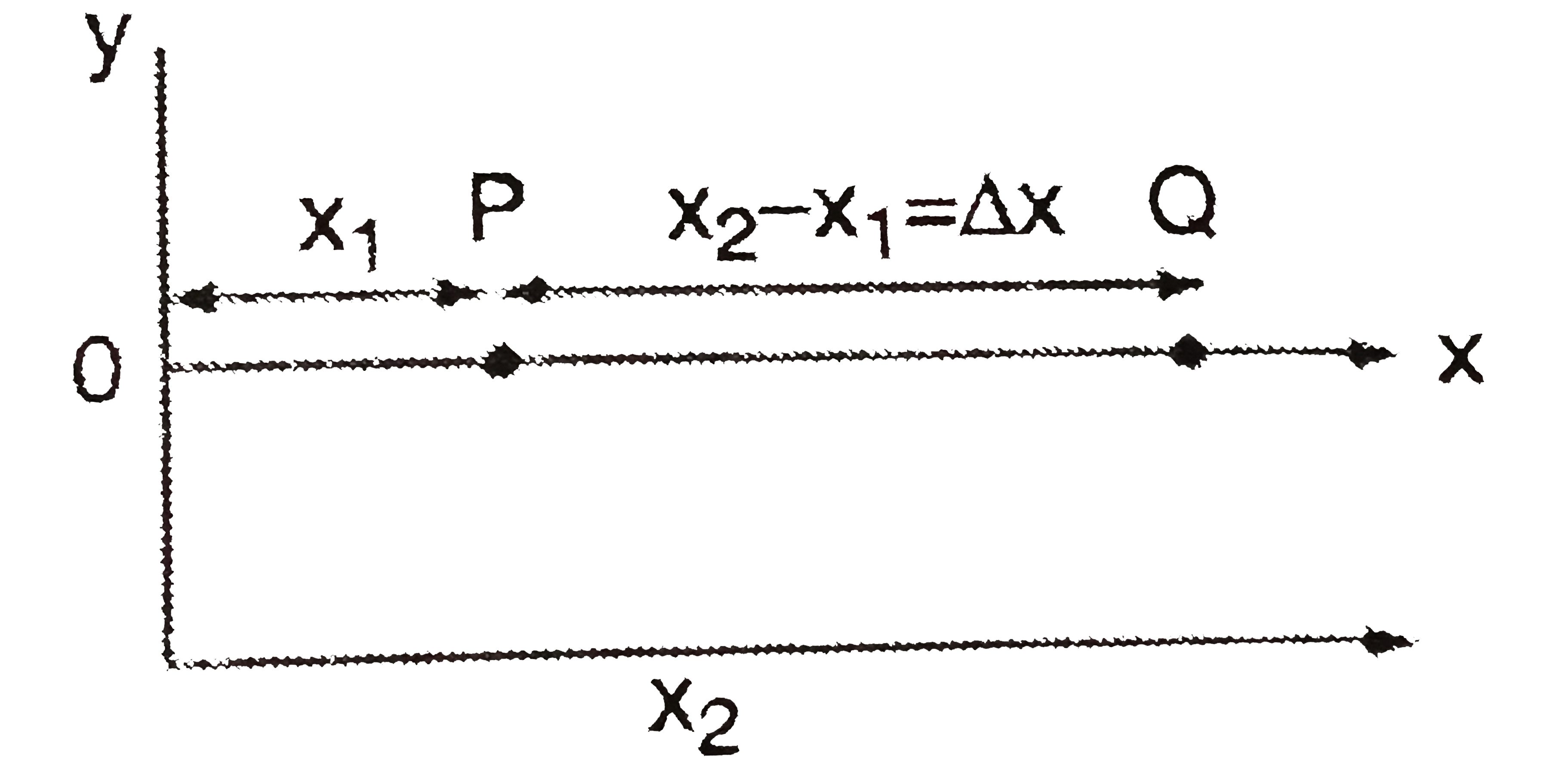
The average velocity ¯¯¯V=x2−x1t2−t1=ΔxΔt
A particle moves half the time of its journey with u. The rest of the half time it moves with two velocities v1 and v2 such that half the distance it covers with v1 and the other half with v2. The net average velocity is: (Assume straight line motion)Au(v1+v2)+2v1v22(v1+v2)B2u(v1+v2)2u+v1+v2Cu(v1+v2)2v1D2v1v2u+v1+v2A particle moves along x - axis in such a way that its x - co - ordinate varies with time according to the equation x=4−2t+t2. The speed of the particle will vary with time as
A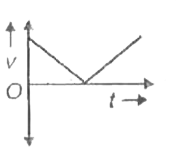 B
B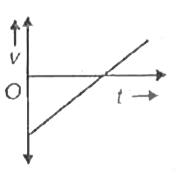 C
C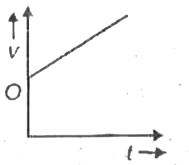 D
D
A particle moves along x-axis in such a way that its x-coordinate varies with time t according to the equation x=(8−4t+6t2) metre.
The velocity of the particle will vary with time according to the graph :-A B
B C
C D
D
(a) A particle is moving along the x axis and its velocity vs position graph is as shown. Is the acceleration of the particle increasing, decreasing or remains constant?
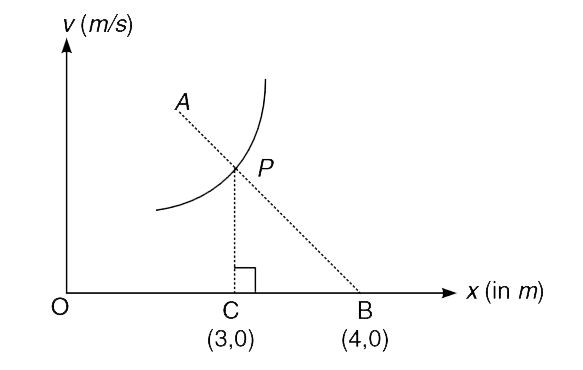
(b) A particle is moving along x axis and its velocity (v) vs position (x) graph is a curve as shown in the figure. Line APB is normal to the curve at point P. Find the instantaneous acceleration of the particle at x=3.0m.
View SolutionA particle is moving in x-y plane with its x and y co-ordinates varying with time as, x=2tandy=10t−16t2. Find trajectory of the particle.
View SolutionConsider the v-t diagram of a particle moving along x axis as shown below.Velocity is in m/s and time is in seconds
View SolutionA particle moves along the x-axis such that its co-ordinate (x) varies with time (t), according to the expression x=2−5t+6t2, where x is in metres and t is in seconds. The initial velocity of the particle is :–
View SolutionA particle moves along x-axis in such a way that its r-coordinate varies with time't according to the equation x= (8−4t+6t2) metre. The velocity of the particle will vary with time according to the graph
View Solution

