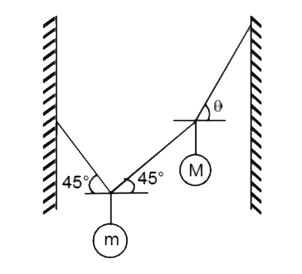
Two spherical objects each of radii R and masses m1 and m2 are suspended using two strings of equal length L as shown in the figure $(R < < L)$ . The angle, $θ$ which mass $m_{2}$ makes with the vertical is approximately -

A

$\frac{m_{1} R}{(m_{1} + m_{2}) L}$

B

$\frac{2 m_{1} R}{(m_{1} + m_{2}) L}$

C

$\frac{2 m_{2} R}{(m_{1} + m_{2}) L}$

D

$\frac{m_{2} R}{(m_{1} + m_{2}) L}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Distance of centre of mass from $m_{2}$
$d = \frac{m_{1}}{(m_{1} + m_{2})} \times 2 R$
$θ = \frac{distance(d)}{L} \Rightarrow θ = \frac{m_{1}}{(m_{1} + m_{2})} \times \frac{2 R}{L}$

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two small metal balls of different mass $m_{1}$ and $m_{2}$ are connected by strings of equal length to a fixed point. When the balls are given equal charges, the angles that the two strings make with the vertical are $30^{\circ}$ and $60^{\circ}$ , respectively. The ratio $m_{1} / m_{2}$ is close to -
A $1.7$
B $3.0$
C $0.58$
D $2.0$
Question 2 - Select One
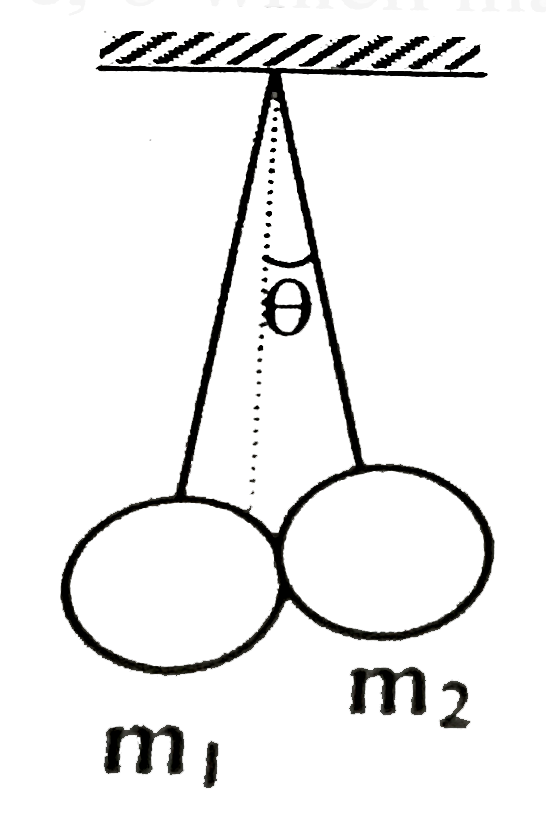
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then

A $tan θ = 1 + \frac{2 M}{m}$
B $tan θ = 1 + \frac{2 m}{M}$
C $cot θ = 1 + \frac{2 M}{m}$
D $cot θ = 1 + \frac{2 m}{M}$
Question 3 - Select One
Two small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle $θ$ that the threads will make with the vertical due to attraction between the balls is :

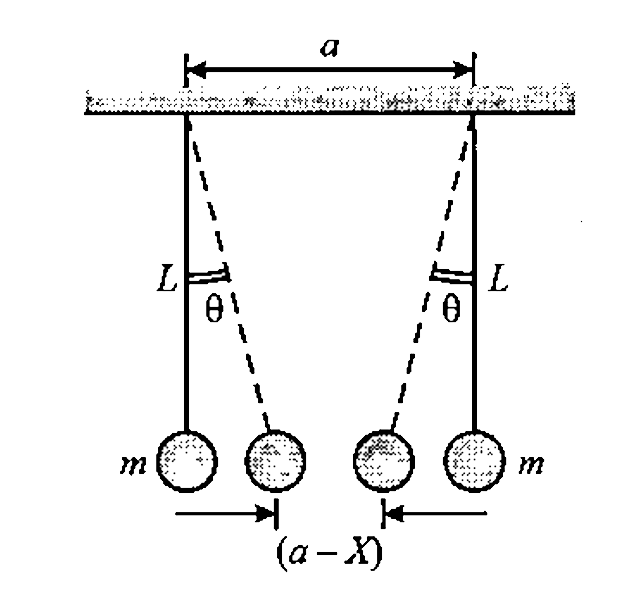A ${tan}^{- 1} \frac{(a - X) g}{m G}$
B ${tan}^{- 1} \frac{m G}{{(a - X)}^{2} g}$
C ${tan}^{- 1} \frac{{(a - X)}^{2} g}{m G}$
D ${tan}^{- 1} \frac{(a^{2} - X^{2}) g}{m G}$

ERRORLESS-NEWTON'S LAWS OF MOTION-NCERT BASED QUESTION (MOTION OF CONNECTED BODIES)

Home
Ask Doubt
Profile