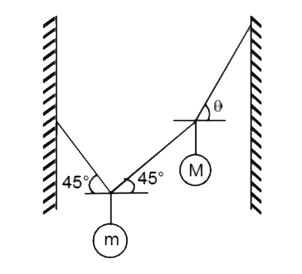
Two masses m1 and m2 are attached with light strings as shown. If the system is in equilibrium, find the value of θ
Ball of mass m1:
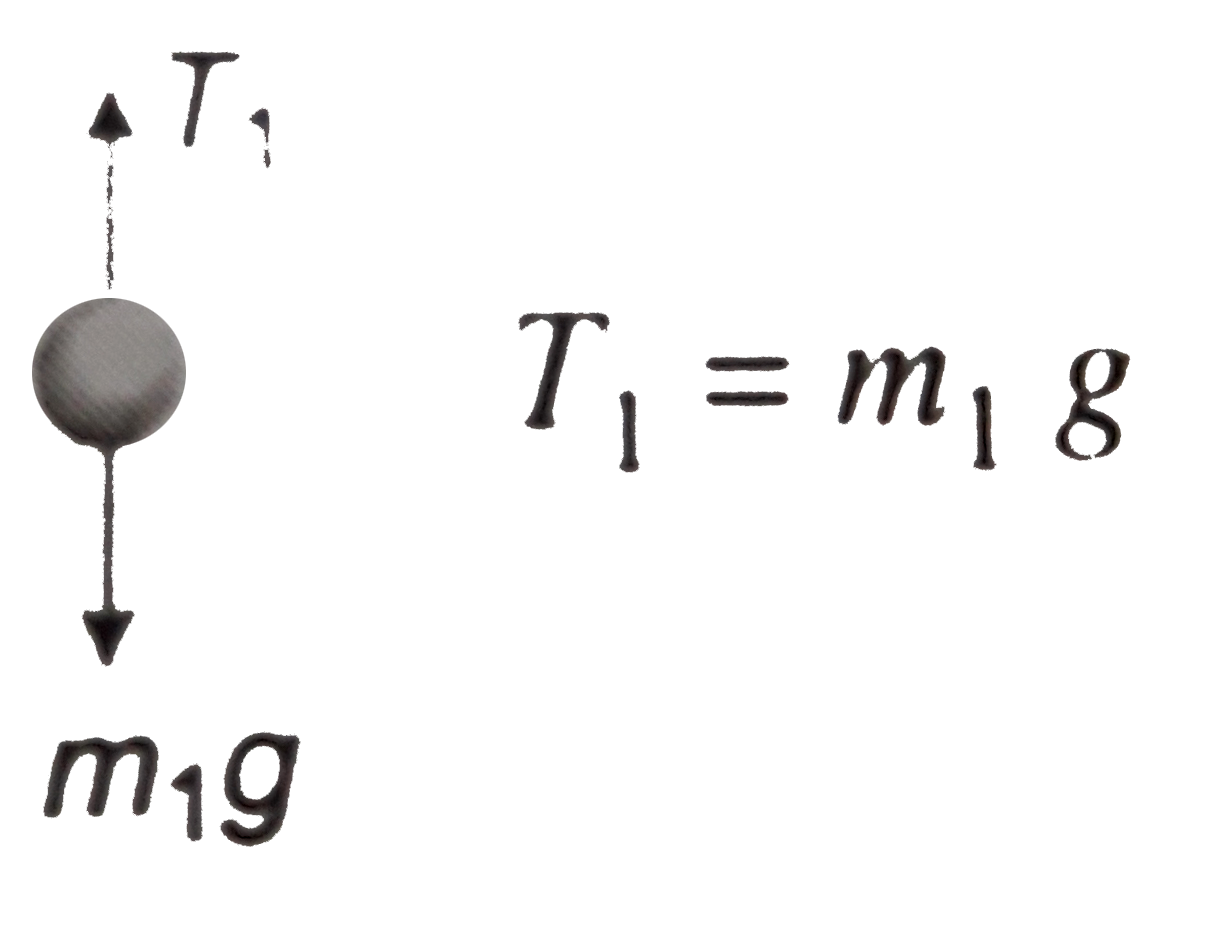
T1=m1g
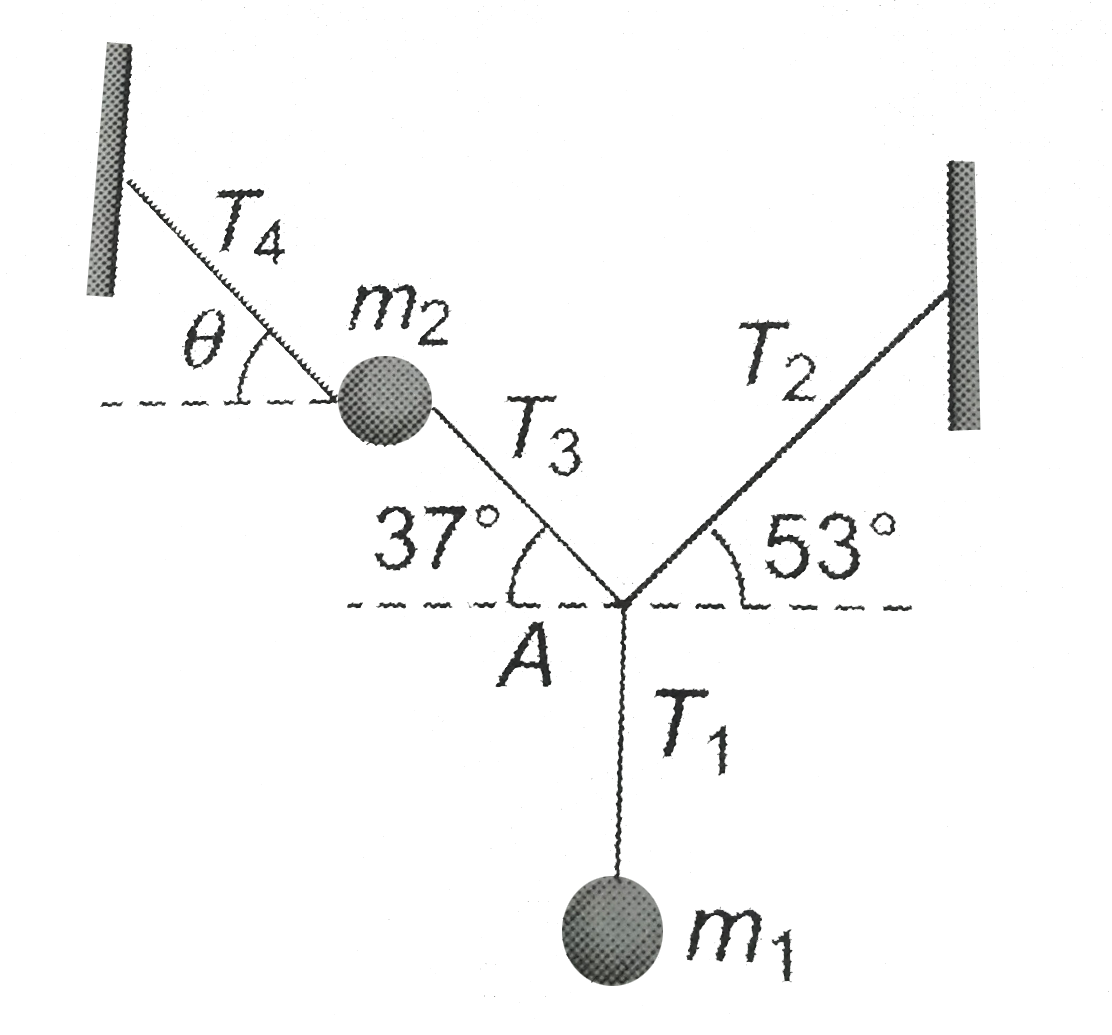
Joint A
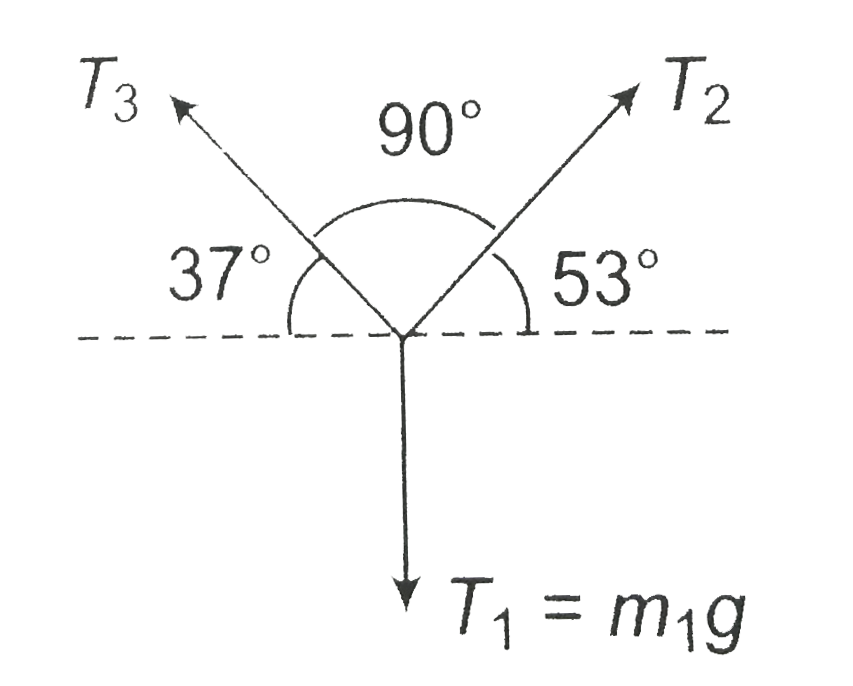
By Lami's theorem
T3sin(90+53∘)=m1gsin(90∘)=T3cos53∘=m1g
⇒T3=m1gcos53∘
T3=3m1g5
Ball of mass m2:
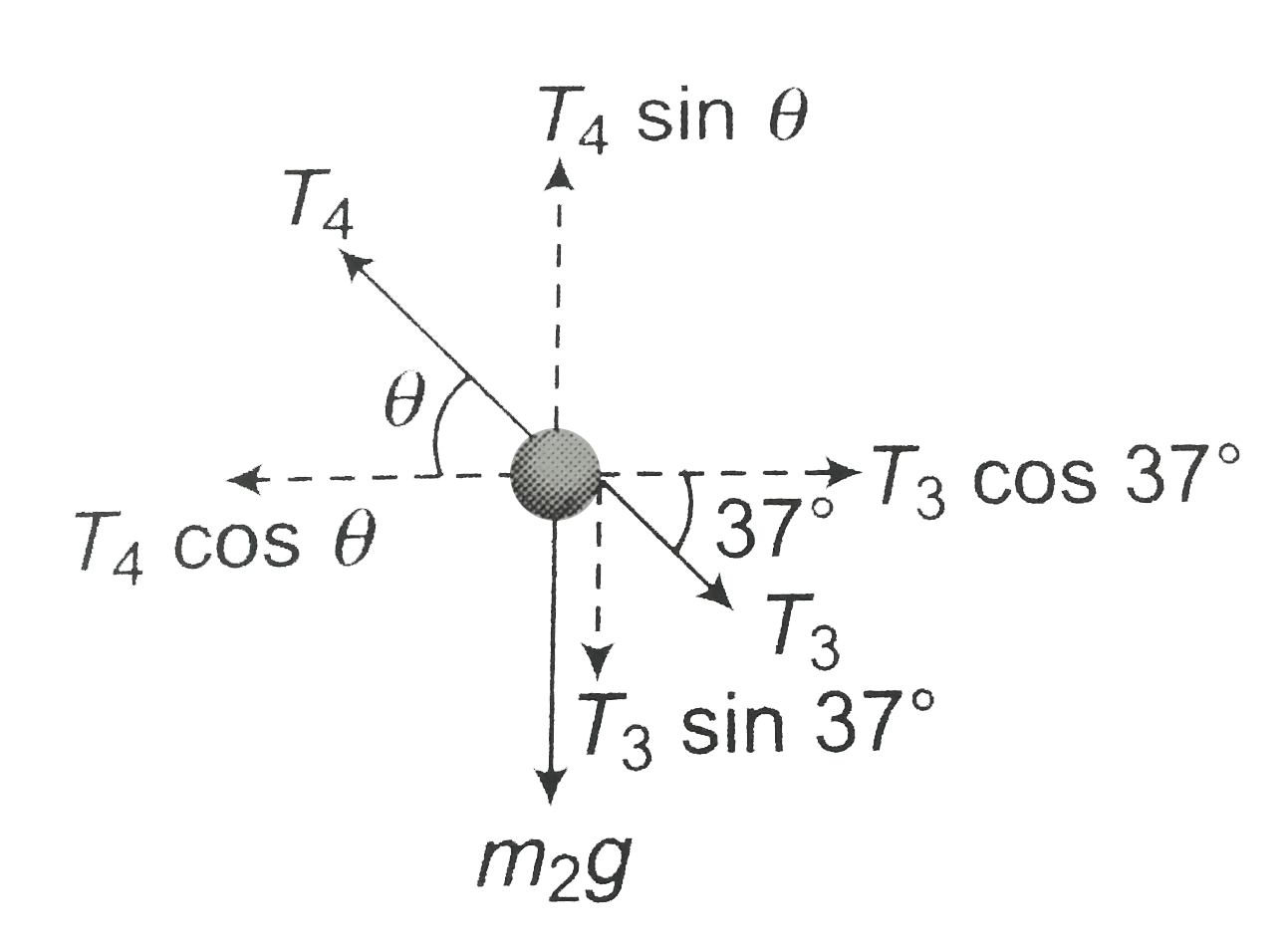
↑:T4sinθ=m2g+T3sin37∘
=m2g+3m1g5×35
=m2g+9m1g25 (i)
←:T4cosθ=T3cos37∘
=3m1g5×45=12m1g25 (ii)
Dividing (i) by (ii), we get
tanθ=m2g+m1g2512m1g25=9m1+25m212m1
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
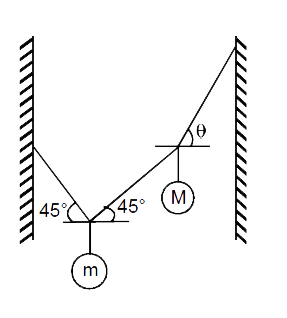 Atanθ=1+2MmBtanθ=1+2mMCcotθ=1+2MmDcotθ=1+2mM
Atanθ=1+2MmBtanθ=1+2mMCcotθ=1+2MmDcotθ=1+2mMTwo masses m and M are attached with strings as shown. For the system to be in equilibrium we have.
 Atanθ=1+2MmBtanθ=1+2mMCtanθ=1+M2mDtanθ=1+m2M
Atanθ=1+2MmBtanθ=1+2mMCtanθ=1+M2mDtanθ=1+m2MTwo objects A and B of masses mA and mB are attached by strings as shown in fig. If they are given upward acceleration then the rato of tension T1:T2 is-
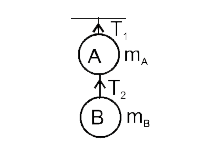 A(mA+mB)/mBB(mA+mB)/mACmA+mBmA−mBDmA−mBmA+mB
A(mA+mB)/mBB(mA+mB)/mACmA+mBmA−mBDmA−mBmA+mB
Three masses m1,m2andm3 are attached to a string -pulley system as shown . All the three masses are held at rest and then released If m3 remains at rest , then

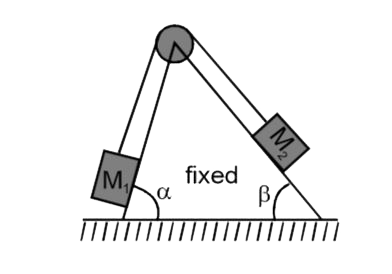
View SolutionTwo masses M1 and M2 are attached to the ends of a light string which passes over a massless pulley attached to the top of a double inclined smooth plane of angles of inclination α and β.The tension in the string is :
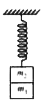
View SolutionTwo masses m1 and m2 are suspended w together by a light spring of spring constant k as shown in figure. When the system is in equilibrium, the mass m1 is removed without disturbing the system. As a result of this removal, mass m2 performs simple harmonic motion. For this situation mark the correct statement(s).
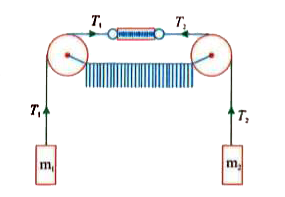
View SolutionTwo masses m1 and m2 are attached to a spring balance S as shown in Figure. If m1>m2 then the reading of spring balance will be
View SolutionIf system is in equilibrium then find relation between m1 and m2
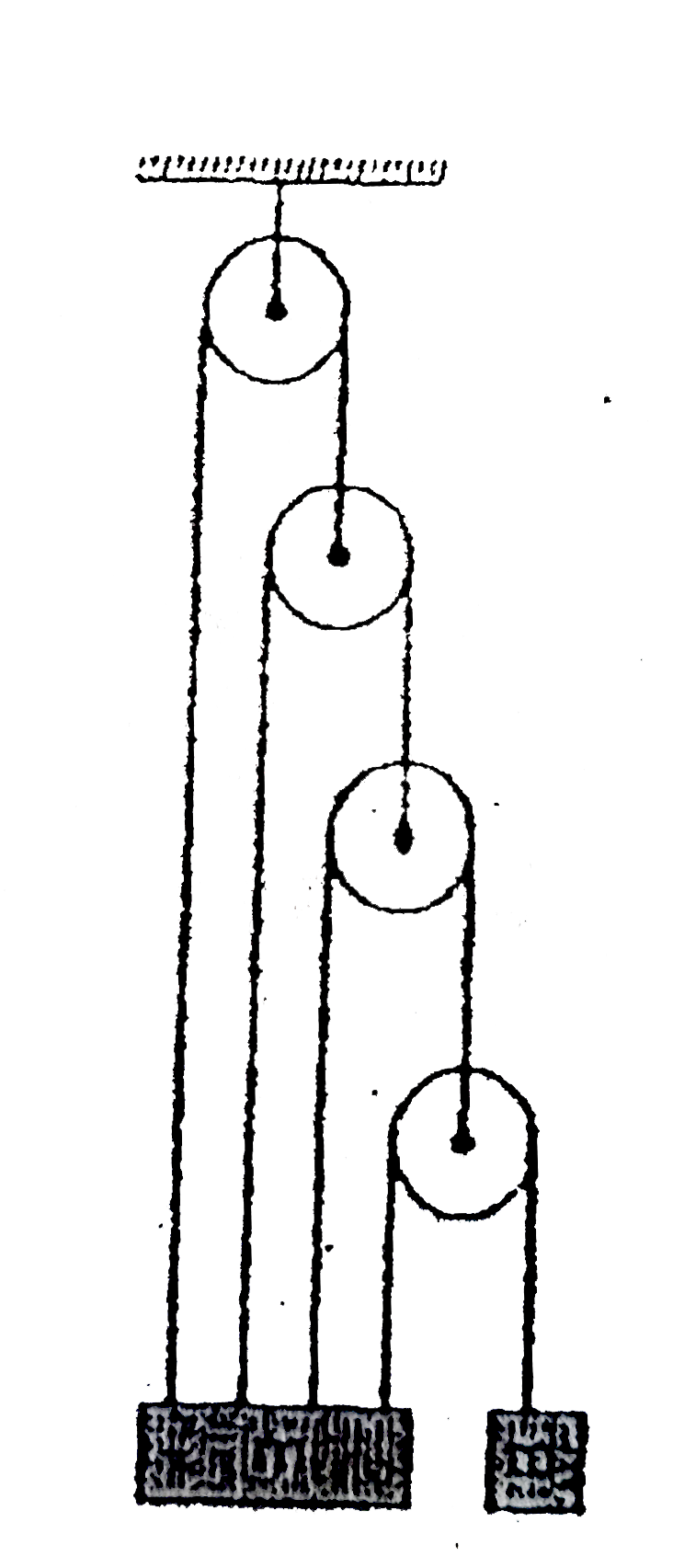
View Solution