Two metallic balls of mass m are suspended by two strings of length L. The distance between upper ends is l. The angle at which the string will be inclined with vertical due to attraction is (m<<M where M is the mass of Earth)
tan−1(Gmgl2
tan−1(GmgL2
tan−1(Gmgl)
tan−1(GmgL)
The correct Answer is:B
To solve the problem of two metallic balls of mass m suspended by strings of length L, with a distance l between their lower ends, we need to find the angle θ that the strings make with the vertical due to the gravitational attraction between the balls.
1. Understanding the Setup:
- We have two metallic balls of mass m suspended by strings of length L.
- The distance between the lower ends of the strings is l.
- The balls will exert a gravitational force on each other, causing the strings to incline at an angle θ with the vertical.
2. Forces Acting on the Balls:
- Each ball experiences two forces:
- The gravitational force acting downwards, which is mg (where g is the acceleration due to gravity).
- The tension T in the string, which can be resolved into two components:
- Vertical component: Tcos(θ)
- Horizontal component: Tsin(θ)
3. Setting Up the Equations:
- For vertical equilibrium (the ball is not moving up or down):
\(
T \cos(θ) = mg \tag{1}
\)
- For horizontal equilibrium (the balls are not moving sideways):
\(
T \sin(θ) = F \tag{2}
\)
where F is the gravitational force of attraction between the two masses.
4. Calculating the Gravitational Force:
- The gravitational force F between the two balls can be calculated using Newton's law of gravitation:
\(
F = \frac{G m^2}{d^2}
\)
where d is the distance between the centers of the two balls. For small angles, we can approximate d in terms of L and θ:
\(
d = 2L \sin(θ) \approx l \quad (\text{for small } θ)
\)
5. Dividing the Equations:
- Dividing equation (2) by equation (1):
\(
\frac{T \sin(θ)}{T \cos(θ)} = \frac{F}{mg}
\)
This simplifies to:
\(
\tan(θ) = \frac{F}{mg}
\)
6. Substituting the Gravitational Force:
- Substituting the expression for F:
\(
\tan(θ) = \frac{G m^2 / l^2}{mg}
\)
- Simplifying gives:
\(
\tan(θ) = \frac{G m}{g l^2}
\)
7. Finding the Angle:
- Finally, we can find the angle θ:
\(
θ = \tan^{-1}\left(\frac{G m}{g l^2}\right)
\)
Final Answer:
The angle θ at which the strings will be inclined with the vertical due to the attraction is:
\(
θ = \tan^{-1}\left(\frac{G m}{g l^2}\right)
\)
- We have two metallic balls of mass m suspended by strings of length L.
- The distance between the lower ends of the strings is l.
- The balls will exert a gravitational force on each other, causing the strings to incline at an angle θ with the vertical.
- Each ball experiences two forces:
- The gravitational force acting downwards, which is mg (where g is the acceleration due to gravity).
- The tension T in the string, which can be resolved into two components:
- Vertical component: Tcos(θ)
- Horizontal component: Tsin(θ)
- For vertical equilibrium (the ball is not moving up or down):
\(
T \cos(θ) = mg \tag{1}
\)
- For horizontal equilibrium (the balls are not moving sideways):
\(
T \sin(θ) = F \tag{2}
\)
where F is the gravitational force of attraction between the two masses.
- The gravitational force F between the two balls can be calculated using Newton's law of gravitation:
\(
F = \frac{G m^2}{d^2}
\)
where d is the distance between the centers of the two balls. For small angles, we can approximate d in terms of L and θ:
\(
d = 2L \sin(θ) \approx l \quad (\text{for small } θ)
\)
- Dividing equation (2) by equation (1):
\(
\frac{T \sin(θ)}{T \cos(θ)} = \frac{F}{mg}
\)
This simplifies to:
\(
\tan(θ) = \frac{F}{mg}
\)
- Substituting the expression for F:
\(
\tan(θ) = \frac{G m^2 / l^2}{mg}
\)
- Simplifying gives:
\(
\tan(θ) = \frac{G m}{g l^2}
\)
- Finally, we can find the angle θ:
\(
θ = \tan^{-1}\left(\frac{G m}{g l^2}\right)
\)
The angle θ at which the strings will be inclined with the vertical due to the attraction is:
\(
θ = \tan^{-1}\left(\frac{G m}{g l^2}\right)
\)
Topper's Solved these Questions
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 3 (Miscellaneous Type Questions)
Explore 20 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 4 A (Conceptual Subjective Exercise)
Explore 14 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 1 (Check your Grasp)
Explore 28 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:subjective
Explore 14 Videos
- KINEMATICS-2DBook:ALLENChapter:KINEMATICS-2DExercise:Exercise (O-2)
Explore 48 Videos
Similar Questions
Two balls of mass m each are hung side by side by side by two long threads of equal length l. If the distance between upper ends is r, show that the distance r' between the centres of the ball is given by gr'2(r−r')=2lGm
View SolutionA block of mass M si suspended by two strings angles θ1 and θ2 with the horizontal. Find the tensions in the strings.

View Solution
Knowledge Check
Two small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :
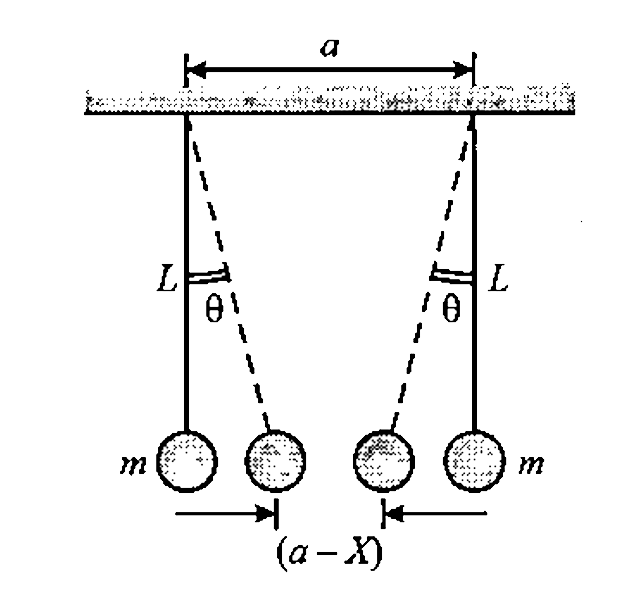 Atan−1(a−X)gmGBtan−1mG(a−X)2gCtan−1(a−X)2gmGDtan−1(a2−X2)gmG
Atan−1(a−X)gmGBtan−1mG(a−X)2gCtan−1(a−X)2gmGDtan−1(a2−X2)gmGA particle of mass m suspended by a string of length l revolves in a horizontal circle such that θ is the angle which the string makes with vertical. Which of the following statement (s) is/are correct ?
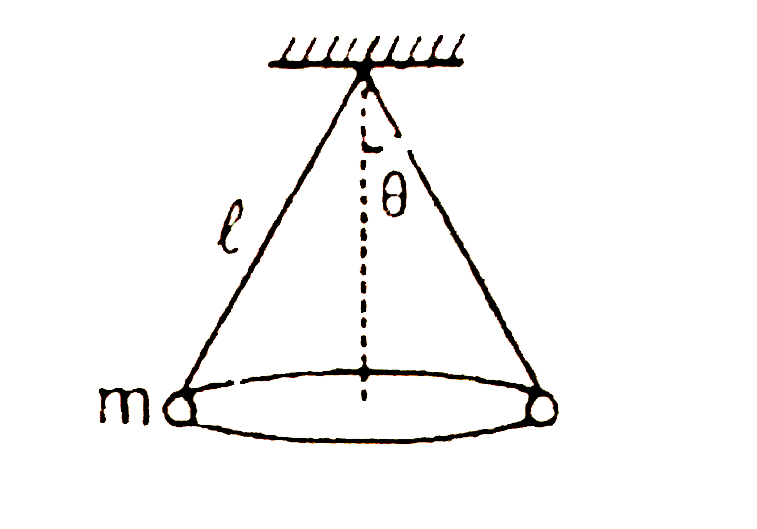 ATension in string =mgcosθBSpeed v of particle =√lgsin2θcosθCTime period of revolution =2π√lcosθgDCentripetal acceleration =gtanθ
ATension in string =mgcosθBSpeed v of particle =√lgsin2θcosθCTime period of revolution =2π√lcosθgDCentripetal acceleration =gtanθA particle of mass m suspended by a string of length l revolves in a horizontal circle (θ is the angle the string makes with vertical). Which of the following statement(s) is // are correct?
ATension in string =mgcosθBSpeed v of particle =√lgsin2θcosθCPeriod T=2π√lcosθgDCentripetal acceleration a=Fsinθm where F is tension
A particle of mass m is suspended by a string of length l from a fixed rigid support. Particle is imparted a horizontal velocity u=√2gl. Find the angle made by the string with the vertical when the acceleration of the particle is inclined to the string by 45∘?
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo spherical objects each of radii R and masses m1 and m2 are suspended using two strings of equal length L as shown in the figure (R<<L). The angle, θ which mass m2 makes with the vertical is approximately -
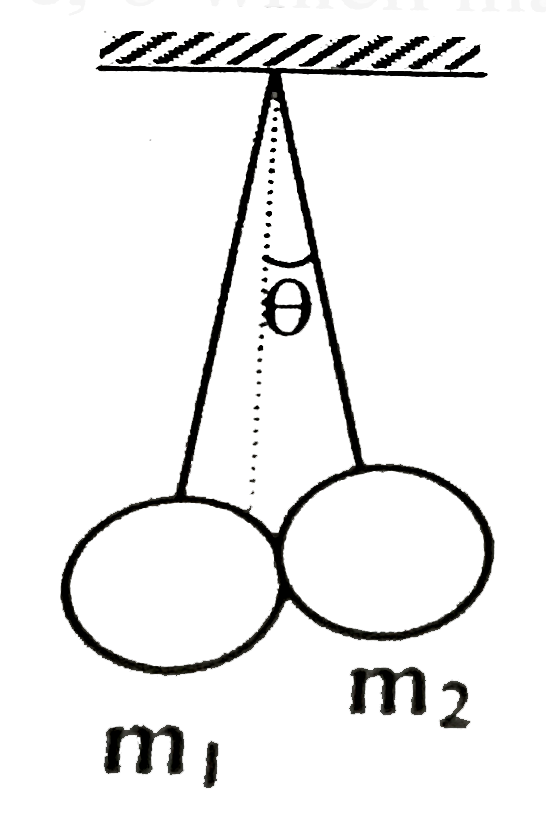
View SolutionTwo point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
View SolutionA stone of mass m is tied to a string and is moved in a vertical circle of radius r making n revolution per minute. The total tension in the string when the stone is its lowest point is.
View Solution

