Question

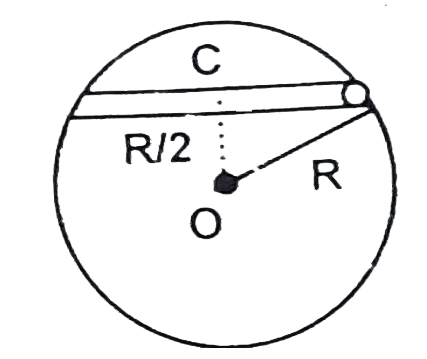
A tunnel is dug along a chord of the earth at a perpendicular distance $R/2$ from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall, and the acceleration of the particle vary with $x$ (distance of the particle from the centre) according to

Options

A.
B.
C.
D.

Answer

B::C

Explanation

Pressing force by the particle on the wall of tunnel is and acceleration is `mgsintheta`
pressing force
`mgcosthetaimplies(GMx)/(R^(3))xx(R)/(2x)implies(GM)/(2R^(2))`
pressing force is independent from 'x' thus it is constant
`gsintheta=(GMx)/(R^(3))sqrt((x^(2)-(R^(2))/(4))/(x^(2)))=(GM)/(2R^(3))sqrt(4x^(2)-R^(2))`
x is increases from `(R)/(2)` to R, thus acceleration increases.