A ball is rolling without slipping in a spherical shallow bowl (radius R) as shown in the figure and is executing simple harmonic motion. If the radius of the ball is doubled, the period of oscillation

Increases slightly
Is reduced by a factor of 1/2
Is increased by a factor of 2
Decreases slightly
The correct Answer is:D
mgsinθ−Fr=ma
Fr=25mr2ar2=a=5gsinθ7R−r⇒ω=√5g7(R−r)
⇒T=2π√7(R−r)5r
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - PAST YEARS QUESTIONS
70 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - ASSERTION AND REASON
25 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Work, Energy and Power)
44 Videos
- NEWTON'S LAWS OF MOTIONBOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason
15 Videos
Similar Questions
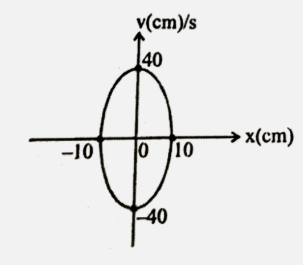
The plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-
View SolutionThe acceleration-displacement (a−X) graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.
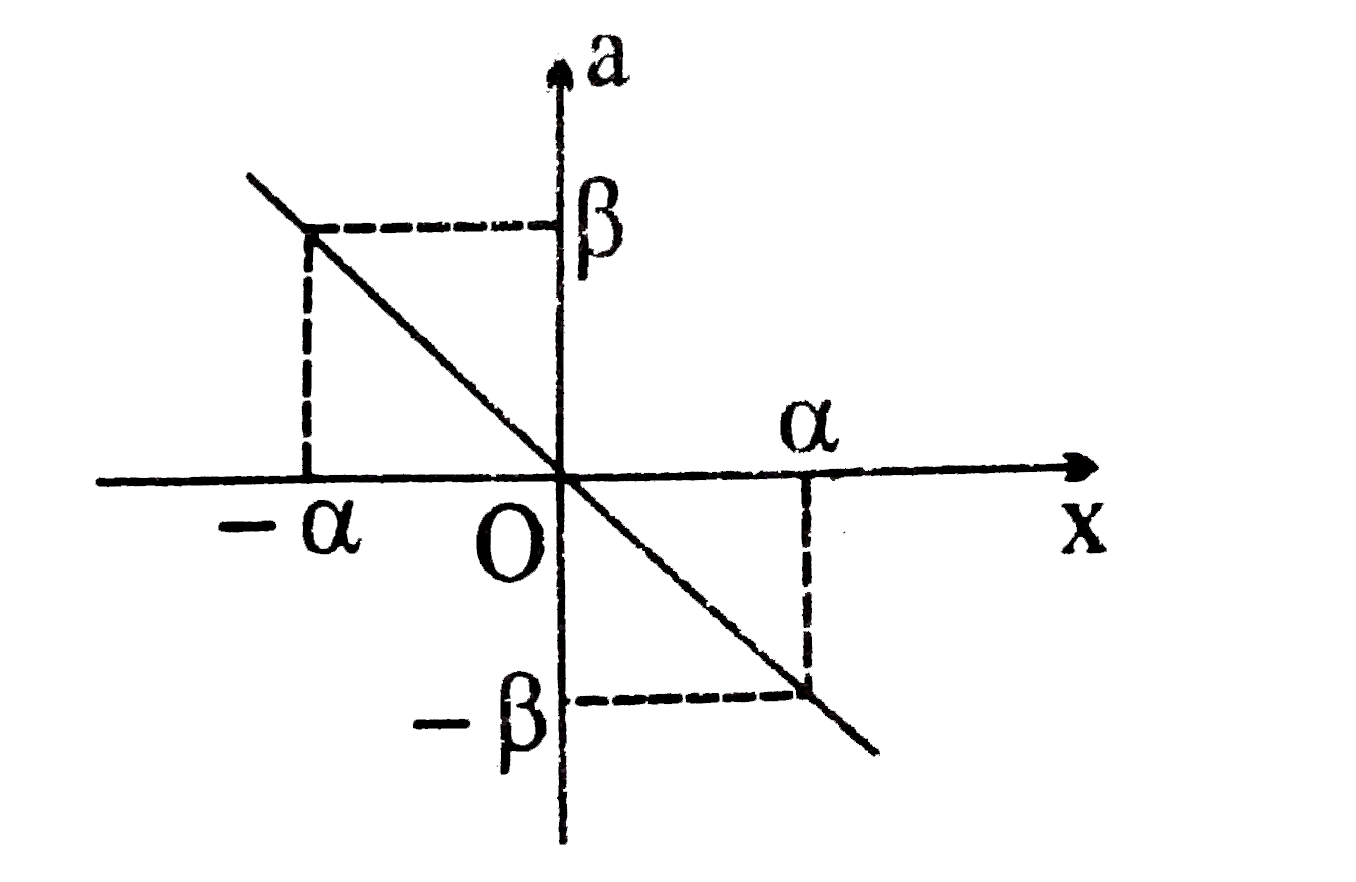
View Solution
Knowledge Check
The maximum velocity a particle, executing simple harmonic motion with an amplitude 7 mm, 4.4 m//s. The period of oscillation is.
A(a) 0.01sB(b) 10sC(c ) 0.1sD(d) 100s
A cylinder of radius R is to roll without slippoing between two planks as shown in the figure. ThenAangular velocity of the cylinder is vR counter clockwiseBangular velocity of the cylinder is 2vR clockwiseCvelocity of centre of mass of the cylinder is v towards leftDvelocity of centre of mass of the cylinder is 2v towards right.A ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is k. If radius of the ball be R, then the fraction of total energy associated with its rotation will be.
Ak2+R2R2Bk2R2Ck2k2+R2DR2k2+R2
The acceleration-displacement graph of a particle executing simple harmonic motion is shown in the figure. The frequency of oscillation is
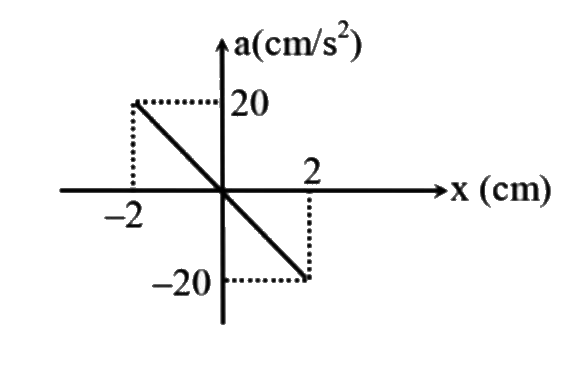
View SolutionWhat is the work done in upturning a thin hemispherical bowl as shown in the figure. The mass of the bowl is M and the radius of the bowl is R.
View SolutionA small sphere S of radius ,r and mass m rolls without slipping, inside a large hemispherical bowl B of radius R as shown in figure. S starts from rest at the top point of the hemisphere
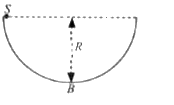
View SolutionA particle executes simple harmonic motion according to equation 4d2xdt2+320x=0. Its time period of oscillation is :-
View SolutionThe acceleration displacement graph of a particle executing simple harmonic motion is shown in figure. The time period of simple harmonic motion is
View Solution