Moment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
52 I
3 I
32 I
2 I
The correct Answer is:A
MR22=I⇒MR2=2I
MOI about a tangent
I.=MR24+MR2=54MR2
implies I.=52I
Topper's Solved these Questions
- ROTATIONAL MOTIONBook:ERRORLESSChapter:ROTATIONAL MOTIONExercise:NCERT BASED QUESTIONS (Angular Momentum)
Explore 52 Videos
- ROTATIONAL MOTIONBook:ERRORLESSChapter:ROTATIONAL MOTIONExercise:NCERT BASED QUESTIONS (Work, Energy and Power)
Explore 44 Videos
- ROTATIONAL MOTIONBook:ERRORLESSChapter:ROTATIONAL MOTIONExercise:NCERT BASED QUESTIONS (Angular Displacement, Velocity and Acceleration)
Explore 34 Videos
- NEWTON'S LAWS OF MOTIONBook:ERRORLESSChapter:NEWTON'S LAWS OF MOTIONExercise:ASSERTION & REASON
Explore 18 Videos
- SIMPLE HARMONIC MOTIONBook:ERRORLESSChapter:SIMPLE HARMONIC MOTIONExercise:Assertion & Reason
Explore 15 Videos
Similar Questions
If I1,I2 ,and I3 are moments of inertia of a disc about its geometric axis,diameter and a tangent in its plane,then
View SolutionAssuming he expression for the moment of inertia of a thin disc about its diameter, show that the moment of inertia of the disc about a tangent in its plane is 54MR2
View Solution
Knowledge Check
Moment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
A52IB3IC32ID2IThe moment of inertia of a solid cylinder about its own axis is the same as its moment of inertia about an axis passing through its centre of gravity and perpendicular to its length. The relation between its length L and radius R is :
AL=√2RBL=√3RCL=3RDL=RThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is
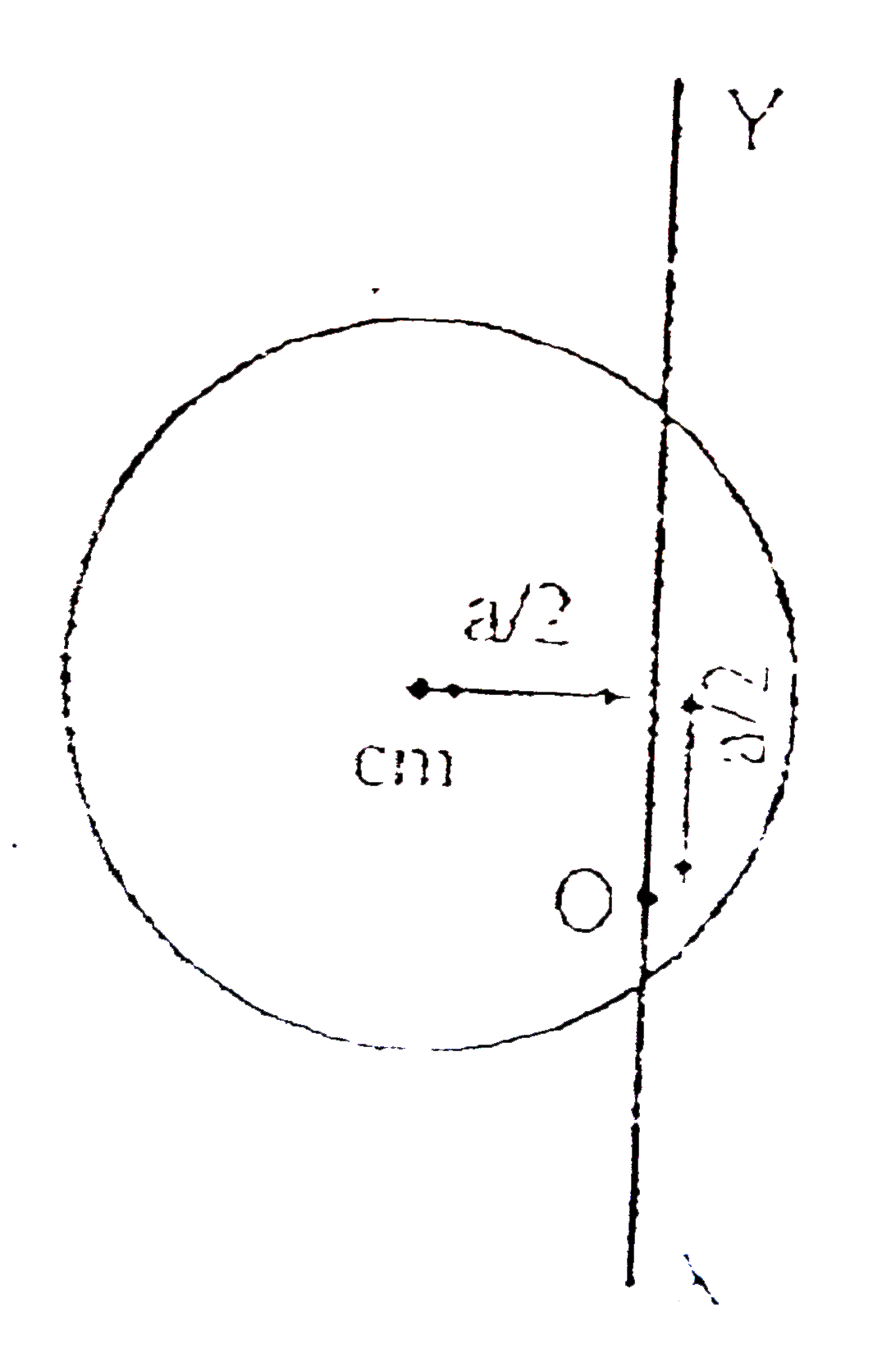 A43Ma2BI+14Ma2C2IDI2
A43Ma2BI+14Ma2C2IDI2
A uniform rectangular plate has moment of inertia about its longer side, equal to I. The moment of inertia of the plate about an axis in its plane, passing through the centre and parallel to the shorter sides is also equal to I. Find its moment of inertia about an axis passing through its centre and perpendicular to its plane.
View SolutionThe Moment of inertia of a disc about an axis passing through its centre and perpendicular to its plane is 1 / 2MR2. Derive the values of moment of inertia of the disc about its diameter and about an axis tangential to the disc lying on its plane ?
View SolutionThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
View SolutionMoment of inertia of a uniform circular disc about a diameter is I. Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be.
View SolutionMoment of inertia of a solid sphere about its diameter is I0 . Then moment of inertia about an axis parallel to its diameter at a distance equal to half of its radius is
View Solution