A rod of length L is composed of a uniform length 1/2 L of wood mass is $m_{w}$ and a uniform length 1/2 L of brass whose mass is $m_{b}$ . The moment of inertia $I$ of the rod about an axis perpendicular to the rod and through its centre is equal to

A

$(m_{ω} + m_{b}) \frac{L^{2}}{12}$

B

$(m_{ω} + m_{b}) \frac{L^{2}}{6}$

C

$(m_{ω} + m_{b}) \frac{L^{2}}{3}$

D

$(m_{ω} + m_{b}) \frac{L^{2}}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

MOI of system
$I = I_{ω} + I_{b}$

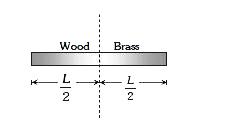
$I = ⎡ ⎢ ⎢ ⎢ ⎣ \frac{m_{ω} {(\frac{L}{2})}^{2}}{12} + m_{ω} {(\frac{L}{4})}^{2} ⎤ ⎥ ⎥ ⎥ ⎦ + ⎡ ⎢ ⎢ ⎢ ⎣ \frac{m_{b} {(\frac{L}{2})}^{2}}{12} + m_{b} {(\frac{L}{4})}^{2} ⎤ ⎥ ⎥ ⎥ ⎦$
$I = \frac{L^{2}}{12} [m_{ω} + m_{b}]$ .

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A light rod of length l has two masses $m_{1}$ and $m_{2}$ attached to its two ends . The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is
A $\frac{m_{1} m_{2}}{m_{1} + m_{2}} l^{2}$
B $\frac{m_{1} + m_{2}}{m_{1} m_{2}} l^{2}$
C $(m_{1} + m_{2}) l^{2}$
D $\sqrt{m_{1} m_{2}} l^{2}$
Question 2 - Select One
A light rod of length $l$ has two masses $m_{1}$ and $m_{2}$ attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
A $(m_{1} + m_{2}) l^{2}$
B $\sqrt{m_{1} m^{2}} l^{2}$
C $\frac{m_{1} m_{2}}{m_{1} + m_{2}} l^{2}$
D $\frac{m_{1} + m_{2}}{m_{1} m_{2}} l^{2}$
Question 3 - Select One
A light rod of length $l$ has two masses $m_{1}$ and $m_{2}$ attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
A $(m_{1} + m_{2}) l^{2}$
B $\sqrt{m_{1} m_{2}} l^{2}$
C $\frac{m_{1} m_{2}}{m_{1} + m_{2}} l^{2}$
D $\frac{m_{1} + m_{2}}{m_{1} m_{2}} l^{2}$

ERRORLESS-ROTATIONAL MOTION-NCERT BASED QUESTIONS (Moment of Inertia)

Home
Ask Doubt
Profile