Moment of inertia of a solid sphere about its diameter is I0 . Then moment of inertia about an axis parallel to its diameter at a distance equal to half of its radius is
8I0/13
13I0/8
7I0/2
2I0/7
The correct Answer is:B
To find the moment of inertia of a solid sphere about an axis parallel to its diameter and at a distance equal to half of its radius, we can use the Parallel Axis Theorem. Here’s the step-by-step solution:
Step 1: Understand the Given Information
We know that the moment of inertia of a solid sphere about its diameter is given as I0. The formula for the moment of inertia of a solid sphere about its diameter is:
I0=25mr2
where m is the mass of the sphere and r is its radius.
Step 2: Identify the New Axis
We need to find the moment of inertia about an axis that is parallel to the diameter and at a distance of r2 from the diameter.
Step 3: Apply the Parallel Axis Theorem
The Parallel Axis Theorem states that:
I=Icm+md2
where:
- I is the moment of inertia about the new axis,
- Icm is the moment of inertia about the center of mass axis (which is I0 in this case),
- m is the mass of the sphere,
- d is the distance between the two axes.
Here, d=r2.
Step 4: Substitute the Values
Substituting the known values into the equation:
I=I0+m(r2)2
Step 5: Calculate m(r2)2
Calculating m(r2)2:
m(r2)2=m⋅r24=mr24
Step 6: Substitute I0
Now substituting I0=25mr2:
I=25mr2+mr24
Step 7: Find a Common Denominator
To combine these fractions, we need a common denominator. The common denominator of 5 and 4 is 20:
I=820mr2+520mr2=1320mr2
Step 8: Express in Terms of I0
Since I0=25mr2, we can express mr2 in terms of I0:
mr2=52I0
Now substituting this back into the equation for I:
I=1320⋅52I0=6540I0=138I0
Final Answer
Thus, the moment of inertia about the desired axis is:
I=138I0
We know that the moment of inertia of a solid sphere about its diameter is given as I0. The formula for the moment of inertia of a solid sphere about its diameter is:
We need to find the moment of inertia about an axis that is parallel to the diameter and at a distance of r2 from the diameter.
The Parallel Axis Theorem states that:
- I is the moment of inertia about the new axis,
- Icm is the moment of inertia about the center of mass axis (which is I0 in this case),
- m is the mass of the sphere,
- d is the distance between the two axes.
Substituting the known values into the equation:
Calculating m(r2)2:
Now substituting I0=25mr2:
To combine these fractions, we need a common denominator. The common denominator of 5 and 4 is 20:
Since I0=25mr2, we can express mr2 in terms of I0:
Thus, the moment of inertia about the desired axis is:
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - II (C.W)
Explore 60 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - II (H.W)
Explore 60 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - I (C.W)
Explore 63 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL - II (H.W.)
Explore 19 Videos
Similar Questions
Knowledge Check
The moment of inertia of a ring about one of its diameters is I.What willbe its moment of inertia about a tangent parallel to the diameter ?
A4IB2IC32 ID3IMoment of inertia I of a solid sphere about an axis parallel to a diameter and at a distance x from it varies as:
A B
B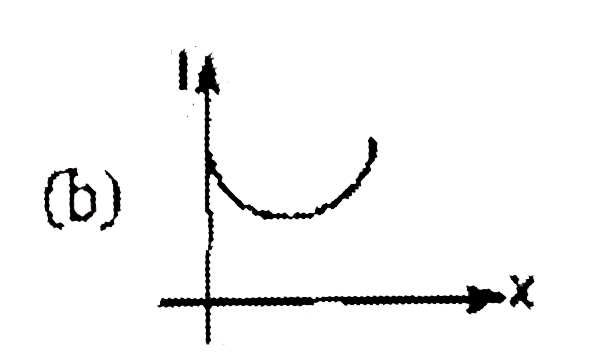 C
C D
D
The moment of inertia of a sphere is 20 kg-m2 about the diameter. The moment of inertia about any tangent is
A25Kgm2B50kgm2C70kgm2D80kgm2
The moment of inertia of a circular ring about one of its diameters is I . What will be its moment of inertia about a tangent parallel to the diameter?
View SolutionThe moment of inertia of a ring about one of its diameter is 2kgm2 . What will be its moment of inertia about a tangent parallel to the diameter?
View SolutionThe moment of inertia of a circular dics about one of its diameters is l. What will be its moment of inertia about a tangent parallel to the diameter?
View SolutionThe moment of inertia of a solid sphere of mass M and radius R about its diameter is I. The moment of inertia of the same sphere about a tangent parallel to the diameter is
View SolutionMoment of inertia of a solid sphere of radius R and density p about its diameter is
View Solution
