A point P on the rim of wheel is intially at rest and in contact with the ground. Find the displacement of the point P if the radius of the wheel is 5 m and the wheel rolls forward through half a revolution
5m
10 m
2.5 m
5(√(π2+4))m
The correct Answer is:D
To solve the problem, we need to find the displacement of point P on the rim of a wheel that rolls forward through half a revolution, given that the radius of the wheel is 5 meters.
1. Understand the Initial Position:
- The point P is initially at rest and in contact with the ground. This means it is at the bottom of the wheel.
2. Determine the Radius:
- The radius of the wheel (r) is given as 5 meters.
3. Calculate the Diameter:
- The diameter (D) of the wheel is twice the radius:
D=2r=2×5=10 meters
4. Identify the Movement:
- When the wheel rolls forward through half a revolution, point P moves from the bottom of the wheel to the top of the wheel.
5. Calculate the Linear Distance Traveled by the Center of Mass:
- During half a revolution, the center of mass of the wheel moves forward by a distance equal to half the circumference of the wheel:
Circumference=2πr=2π×5=10π meters
Distance traveled=12×10π=5π meters
6. Determine the Final Position of Point P:
- After half a revolution, point P is now at the top of the wheel. The center of mass has moved forward by 5π meters, and point P is now vertically above the center of mass at a height equal to the radius (5 meters).
7. Use the Pythagorean Theorem to Find Displacement:
- The displacement (S) is the straight-line distance from the initial position of point P (at the bottom) to its final position (at the top). This forms a right triangle where:
- One leg is the vertical distance (the radius) = 5 meters.
- The other leg is the horizontal distance (distance traveled by the center of mass) = 5π meters.
- Using the Pythagorean theorem:
S=√(5π)2+(5)2
S=√25π2+25=√25(π2+1)=5√π2+1
8. Final Calculation:
- Substitute the value of r (5 meters) into the displacement formula:
S=5√π2+1 meters
Final Answer:
The displacement of point P after the wheel rolls forward through half a revolution is:
S=5√π2+1 meters
- The point P is initially at rest and in contact with the ground. This means it is at the bottom of the wheel.
- The radius of the wheel (r) is given as 5 meters.
- The diameter (D) of the wheel is twice the radius:
D=2r=2×5=10 meters
- When the wheel rolls forward through half a revolution, point P moves from the bottom of the wheel to the top of the wheel.
- During half a revolution, the center of mass of the wheel moves forward by a distance equal to half the circumference of the wheel:
Circumference=2πr=2π×5=10π meters
Distance traveled=12×10π=5π meters
- After half a revolution, point P is now at the top of the wheel. The center of mass has moved forward by 5π meters, and point P is now vertically above the center of mass at a height equal to the radius (5 meters).
- The displacement (S) is the straight-line distance from the initial position of point P (at the bottom) to its final position (at the top). This forms a right triangle where:
- One leg is the vertical distance (the radius) = 5 meters.
- The other leg is the horizontal distance (distance traveled by the center of mass) = 5π meters.
- Using the Pythagorean theorem:
S=√(5π)2+(5)2
S=√25π2+25=√25(π2+1)=5√π2+1
- Substitute the value of r (5 meters) into the displacement formula:
S=5√π2+1 meters
The displacement of point P after the wheel rolls forward through half a revolution is:
S=5√π2+1 meters
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Moment of Inertia)
139 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Momentum)
52 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - Assertion & Reason
25 Videos
- NEWTON'S LAWS OF MOTIONBOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason
15 Videos
Similar Questions
What is the displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward half a revolution? Take the radius of the wheel as R and the x-axis as the forward direction?
View SolutionA wheel makes 1000 revolutions in covering a distance of 88 km. Find the radius of the wheel.
View Solution
Knowledge Check
The displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward quarter revolution where perimeter of the wheel is 4πm, is (Assume the forward direction as x-axis)
A√(π+2)2+4along tan−12π with x-axisB√(π+2)2+4along tan−12π−2 with x-axisC√(π+2)2+4along tan−12π with x-axisD√(π+2)2+4along tan−12π−2 with x-axisA wheel makes 4000 revolutions in moving a distance of 44 km. Find the radius of the wheel.
A15 mB27 mC25 mD1. 75 mA flywheel of diameter 1 m is rotating at 600 r.p.m., the acceleration of a point on the rim of the fly wheel is
A100π2m/s2B150π2m/s2C200π2m/s2D300π2m/s2
A wheel makes 1000 revolutions in covering a distance of 88 km. Find the radius of the wheel.
View SolutionA wheel makes 4000 revolutions in moving a distance of 44 km. Find the radius of the wheel.
View SolutionThe angular velocity of a wheel is 70rad/sec . If the radius of the wheel is 0.5 m , then linear velocity of the wheel is
View SolutionA wheel of radius 1m rolls forward half a revolution on a horizontal ground. The magnitude of the displacement of the point of the wheel initially on contact with the ground is.
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
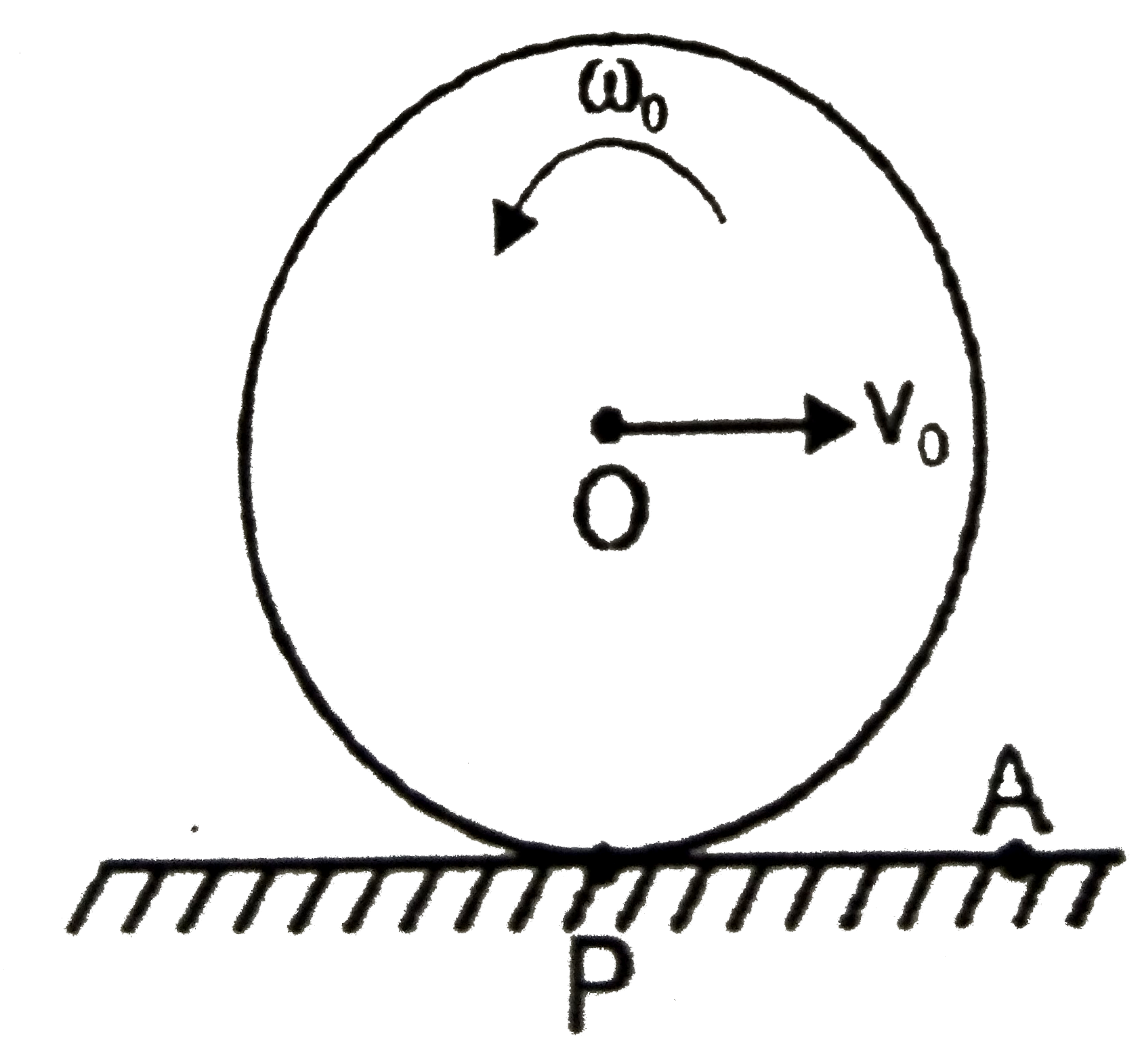
If the wheel comes to permanent rest after sometimes, then :
View Solution
