A wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
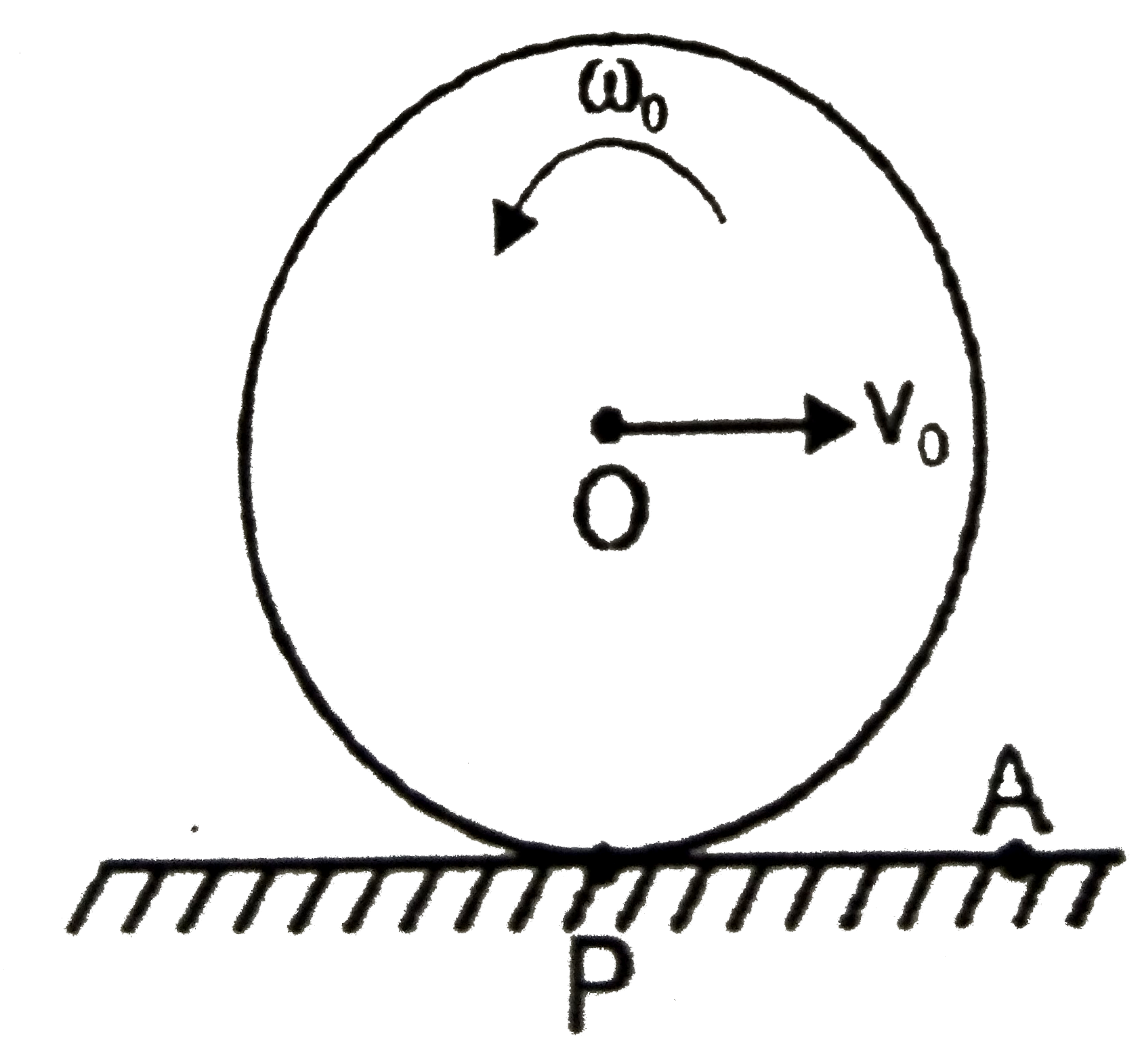
If the wheel comes to permanent rest after sometimes, then :
v0=ω0r
v0=ω0k2r
v0=ω0r2R
V0=ω0(r+k2r)
The correct Answer is:B
Torque of friction about A is zero.
Anglar momentum conservation about point A.
Lin=mv0r−mk2ω
Lfin=0
Lfin=Lin
⇒v0=ωk2/r
Similar Questions
प्रारम्भ में पृथ्वी के सम्पर्क में स्थित 1 m त्रिज्या वाले पहिये के किसी बिन्दु का विस्थापन क्या होगा जब पहिया क्षैतिजत: आगे की ओर आधा चक्कर लगाता हो
View Solutionr त्रिज्या वाले एक पहिए की परिधि पर पतली रस्सी लपेटी हुई है। पहिए का अक्ष क्षैतिज है जिसके परितः इसका जड़त्व आघूर्ण । है। भार mg, रस्सी के सिरे पर बँधा हुआ है जो विरामावस्था से नीचे गिरता है। h दूरी से गिरने के पश्चात् पहिए का कोणीय वेग होगा
View SolutionA wheel of one meter radius rotates halfway across the horizontal plane. The displacement of the wheel point that was previously in contact with the horizontal plane is
View Solutionr त्रिज्या की एक पहिया सरल रेखा में गति कर रहा है। इसके केन्द्र का वेग v है। किसी क्षण पहिये का धरातल से सम्पर्क बिन्दु M एवं पहिया का उच्चतम बिन्दु N(M के व्यस्त विपरित) है। असत्य कथन होगा-
View SolutionA wheel of radius R rolls on the ground with a uniform velocity v. The relative acceleration of topmost point of the wheel with respect to the bottommost point is:
View Solutionएक पहिये को एक खुरदरी क्षैतिज सतह पर प्रारम्भिक क्षैतिज वेग v0 एवं कोणीय वेग ω0 देकर नीचे चित्र में दर्शाये अनुसार छोड़ा जाता है। बिन्दु O पहिये का द्रव्यमान केन्द्र है एवं बिन्दु P इसका सतह के साथ तात्क्षणिक सम्पर्क बिन्दु है। पहिये की त्रिज्या r है तथा इसकी घूर्णन त्रिज्या बिन्दु O के परितः k है। सतह (जमीन) व पहिये के मध्य घर्षण गुणांक μ है। A जमीन पर स्थिर (fixed) बिन्दु है।
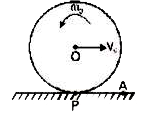
यदि कुछ समय पश्चात् पहिया स्थायी विराम पर आ जाता है तो :
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v_(0) and angular velocity omega_(0) as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k . Coefficient of friction between wheel and ground is mu . A is a fixed point on the ground. Which of the following is conserved ?
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.

If the wheel comes to permanent rest after sometimes, then :
View Solution

