A wheel of radius 1m rolls forward half a revolution on a horizontal ground. The magnitude of the displacement of the point of the wheel initially on contact with the ground is.
π
2π
√2π
√π2+4
The correct Answer is:D
To solve the problem of finding the magnitude of the displacement of the point of the wheel initially in contact with the ground after it rolls forward half a revolution, we can follow these steps:
1. Identify the Initial Position:
The wheel has a radius of 1m. Initially, the point of contact with the ground is at the bottom of the wheel.
2. Determine the Final Position After Half a Revolution:
After rolling half a revolution, the point that was initially in contact with the ground will move to the top of the wheel. The distance traveled by the wheel along the ground during this half revolution is equal to half the circumference of the wheel.
3. Calculate the Distance Traveled:
The circumference of the wheel is given by the formula:
\(
C = 2\pi r
\)
For a radius of 1m, the circumference is:
\(
C = 2\pi \times 1 = 2\pi \text{ m}
\)
Therefore, the distance traveled during half a revolution is:
\(
\text{Distance} = \frac{1}{2} \times C = \frac{1}{2} \times 2\pi = \pi \text{ m}
\)
4. Visualize the Displacement:
The initial position of the point is at (0,0) (the bottom of the wheel), and after half a revolution, it moves to the top of the wheel at (0,2) (since the height of the wheel is equal to its diameter, which is 2m).
5. Calculate the Displacement:
The displacement is the straight-line distance from the initial position to the final position. Using the coordinates:
- Initial position: (0,0)
- Final position: (π,2)
The displacement can be calculated using the Pythagorean theorem:
\(
\text{Displacement} = \sqrt{(\Delta x)^2 + (\Delta y)^2}
\)
where:
- \(\Delta x = \pi - 0 = \pi\)
- \(\Delta y = 2 - 0 = 2\)
Therefore, the displacement is:
\(
\text{Displacement} = \sqrt{(\pi)^2 + (2)^2} = \sqrt{\pi^2 + 4}
\)
6. Final Answer:
The magnitude of the displacement of the point of the wheel initially in contact with the ground after rolling forward half a revolution is:
\(
\sqrt{\pi^2 + 4} \text{ m}
\)
The wheel has a radius of 1m. Initially, the point of contact with the ground is at the bottom of the wheel.
After rolling half a revolution, the point that was initially in contact with the ground will move to the top of the wheel. The distance traveled by the wheel along the ground during this half revolution is equal to half the circumference of the wheel.
The circumference of the wheel is given by the formula:
\(
C = 2\pi r
\)
For a radius of 1m, the circumference is:
\(
C = 2\pi \times 1 = 2\pi \text{ m}
\)
Therefore, the distance traveled during half a revolution is:
\(
\text{Distance} = \frac{1}{2} \times C = \frac{1}{2} \times 2\pi = \pi \text{ m}
\)
The initial position of the point is at (0,0) (the bottom of the wheel), and after half a revolution, it moves to the top of the wheel at (0,2) (since the height of the wheel is equal to its diameter, which is 2m).
The displacement is the straight-line distance from the initial position to the final position. Using the coordinates:
- Initial position: (0,0)
- Final position: (π,2)
\(
\text{Displacement} = \sqrt{(\Delta x)^2 + (\Delta y)^2}
\)
where:
- \(\Delta x = \pi - 0 = \pi\)
- \(\Delta y = 2 - 0 = 2\)
\(
\text{Displacement} = \sqrt{(\pi)^2 + (2)^2} = \sqrt{\pi^2 + 4}
\)
The magnitude of the displacement of the point of the wheel initially in contact with the ground after rolling forward half a revolution is:
\(
\sqrt{\pi^2 + 4} \text{ m}
\)
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:AIIMS Questions
Explore 40 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Chapter Test
Explore 29 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Assertion Reasoning
Explore 20 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Chapter Test
Explore 30 Videos
Similar Questions
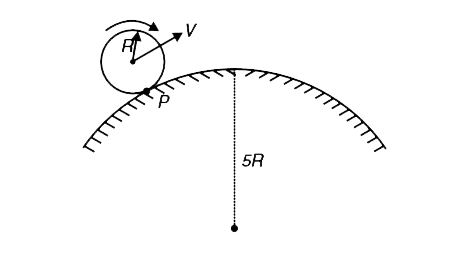
A convex surface has a uniform radius of curvature equal to 5R. A wheel of radius R is rolling without sliding on it with a constant speed v. Find the acceleration of the point (P) of the wheel which is in contact with the convex surface.
View SolutionA wheel of radius 2.1 m of a vehicle makes
75 revolutions in one minute. What is the
speed of the vehicle ?
View Solution
Knowledge Check
A wheel of radius R rolls without slipping on a horizontal ground. The distance travelled by a point on the rim in one complete rotation is:
A2πRB8RC2RDπRA sphere of radius R is rolling on a rough horizontal surface. The magnitude of velocity of A with respect to ground will be
 A√2vCMB2VCMsinθC√2vCM√1+sinθDNo sufficient information
A√2vCMB2VCMsinθC√2vCM√1+sinθDNo sufficient informationIf acycle wheel of radius 0.4 m completes one revolution in one second , then the acceleration of a point on the rim is in one second , then the acceleration of a point on the rim is
A0.8π2m/s2B1.2π2m/s2C1.6π2m/s2D0.4πm/s2
A wheel of circumference C is at rest on the ground. When the wheel rolls forward through half a revolution, then the displacement of initial point of contact will be
View SolutionA wheel of radius R is rolling without sliding uniformly on a horizontal surface. Find the radius of curvature of the path of a point on its circumference when it is at highest point in its path.
View SolutionA disc of mass M and radius R is rolling with angular speed ω on a horizontal plane. The magnitude of angular momentum of the disc about a point on ground along the line of motion of disc is :
View SolutionA wheel of radius R rolls on the ground with a uniform velocity v. The relative acceleration of topmost point of the wheel with respect to the bottommost point is:
View SolutionA cycle wheel of radius 0.4 m completes one revolution in one second then the acceleration of a point on the cycle wheel will be
View Solution

