A bar of length l carrying a small mass m at one of its ends rotates with a uniform angular speed $ω$ in a vertical plane about the mid-point of the bar . During the rotation, at some instant of time when the bar is horizontal, the mass is detached from the bar but the bar continues to rotate with same $ω$ . The mass moves vertically up, comes back and reaches the bar at the same point. At that place, the acceleration due to gravity is g

A

This is possible if the quantity $\frac{ω^{2} l}{2 π g}$ is an integer

B

The total time of flight of the mass is proportional to $ω^{2}$

C

The total distance travelled by the mass in air is proportional to $ω^{2}$

D

The total distance travelled by the mass in air and its total time of flight are both independent on its mass

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C, D

Velocity
$v = \frac{l}{2} ω$
$T = \frac{2 v}{g} = \frac{l ω}{g}$

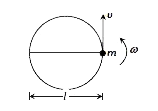
Let no. of rotation = n (within T times)
$n T = \frac{I ω}{g}$
$\Rightarrow n . \frac{2 π}{ω} = \frac{l ω}{g} \Rightarrow n = \frac{l ω^{2}}{2 π g}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A bar of length l canying a small mass m at one of its ends rotates with a uniform angular speed $ω$ in a vertical plane about the mid-point of the bar. During the rotation, at some instant of time when the bar is horizontal, the mass is detached from the bar but the bar continues to rotate with same $ω$ . The mass moves ve1tically up, comes back and reaches the bar at the same point. At that place, the acceleration due to gravity is g.
Athis is possible if the quantity $\frac{ω^{2} l}{2 π g}$ is an integer
Bthe total time of flight of the mass is proportional to $ω^{2}$
Cthe total distance travelled by the mass in air is proportional to $ω^{2}$
Dthe total distance travelled by the mass in air and its total time of flight are both independent of its mass.
Question 2 - Select One
A particle of mass m rotates with a uniform angular speed $ω$ . It is viewed from a frame rotating about the Z-axis with a uniform angular speed $ω_{0}$ . The centrifugal force on the particler is
A $m ω^{2} a$
B $m ω_{0}^{2} a$
C $m {(\frac{ω + ω_{0}}{2})}^{2} a$
D $m ω ω_{0} a$
Question 3 - Select One
A solid cylinder of mass M and radius R rotates about its axis with angular speed $ω$ . Its rotational kinetic energy is
A $\frac{1}{2} M R^{2} ω^{2}$
B $M R^{2} ω^{2}$
C $\frac{1}{4} M R^{2} ω^{2}$
D $\frac{1}{8} M R^{2} ω^{2}$

ERRORLESS-ROTATIONAL MOTION-NCERT BASED QUESTIONS (Angular Momentum)

Home
Ask Doubt
Profile