Assertion: Vector product of two vectors is an axial vector.
Reason: If →v= instantaneous Velocity, →r= radius vector and →ω= angular velocity, then →ω=→v×→r.
If both assertion and reason are true and the reason is the correct explanation of the assertion.
If both assertion and reason are true but reason is not the correct explanation of the assertion
If assertion is true but reason is false.
If the assertion and reason both are false.
The correct Answer is:C
Linear velocity (→v)=→ω×→r
So, →ω=→v×→r is wrong.
Topper's Solved these Questions
Similar Questions
If →a is a non-zero vector and →a.→b=→a.→c,→a×→b=→a×→c, then
View SolutionThe linear velocity of a rotating body is given by →v=→ω×→r, where →ω is the angular velocity and →r is the radius vector. The angular velocity of a body is →ω=ˆi−2ˆj+2ˆk and the radius vector →r=4ˆj−3ˆk, then |→v| is
View Solution
Knowledge Check
- Question 1 - Select One
The cross product of two vectors gives a vector perpendicular to the plane containing the vectors.
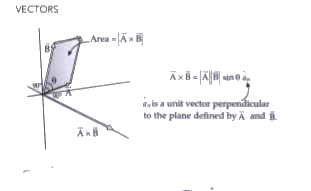
If →a and →b are non-zero vectors, then →a⋅(→a×→b)= _________A0B→0C→aD→b - Question 2 - Select One
The vector product of two vectors →Aand→B is zero. The scalar product of →Aand(→A+→B) will be
AzeroBA2CABDA2+AB - Question 3 - Select One
The linear velocity of a rotating body is given by →v=→ω×→r, where →ω is the angular velocity and →r is the radius vector. The angular velocity of a body is →ω=ˆi−2ˆj+2ˆk and the radius vector →r=4ˆj−3ˆk, then |→v| is-
A√29 unitsB√31 unitsC√37 unitsD√41 units
In nonuniform circular motion, the linear acceleration →a, the angular acceleration, →α, the angular velocity →v the radius vector →r and the angular velocity →ω at any instant are related by the vector equation,
View SolutionThe cross product of two vectors gives a vector perpendicular to the plane containing the vectors.
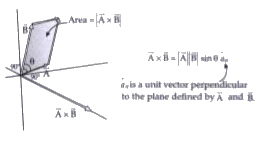
The angle between →a×→b and →b×→a is ___________.View SolutionIf →u and →v are unit vectors and θ is the actue angle between them, then 2→u×3→v is a unit vector for
View SolutionThe resultant of two vectors →P and →Q is →R. If →Q is doubled then the new resultant vector is perpendicular to →P. Then magnitude of →R is :-
View SolutionIf for two vectors →A and →B,→A×→B=0, the vectors
View Solution
