In nonuniform circular motion, the linear acceleration →a, the angular acceleration, →α, the angular velocity →v the radius vector →r and the angular velocity →ω at any instant are related by the vector equation,
→a=→α×→r+→ω×→v
→a=→r×→α+→v×→ω
→a=→α×r+→v×→ω
→a=→α×r−→ω×→v
The correct Answer is:A
Step by step video, text & image solution for In nonuniform circular motion, the linear acceleration vec a, the angular acceleration, vec alpha, the angular velocity vec v the radius vector vec r and the angular velocity vec omega at any instant are related by the vector equation, by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The relation between linear speed v, angular speed ω and angular acceleration α in circular motion is
Aα=aωvBα=avωCα=vωaDα=ωavThe linear velocity of a rotating body is given by →v=→ω×→r, where →ω is the angular velocity and →r is the radius vector. The angular velocity of a body is →ω=ˆi−2ˆj+2ˆk and the radius vector →r=4ˆj−3ˆk, then |→v| is-
A√29 unitsB√31 unitsC√37 unitsD√41 unitsThe linear velocity of a rotating body is given by →v=→ω×→r, where →ω is the angular velocity and →r is the radius vector. The angular velocity of a body is →ω=ˆi−2ˆj+2ˆk and the radius vector →r=4ˆj−3ˆk, then |→v| is
A√29unitsB√31unitC√37unitD√41unit
Angular momentum of a rigid body rotating about a fixed Axis with angular velocity →ω
View SolutionIf →a is a unit vector, →a×→r=→b,→a⋅→r=c,→a⋅→b=0, then →r is equal to
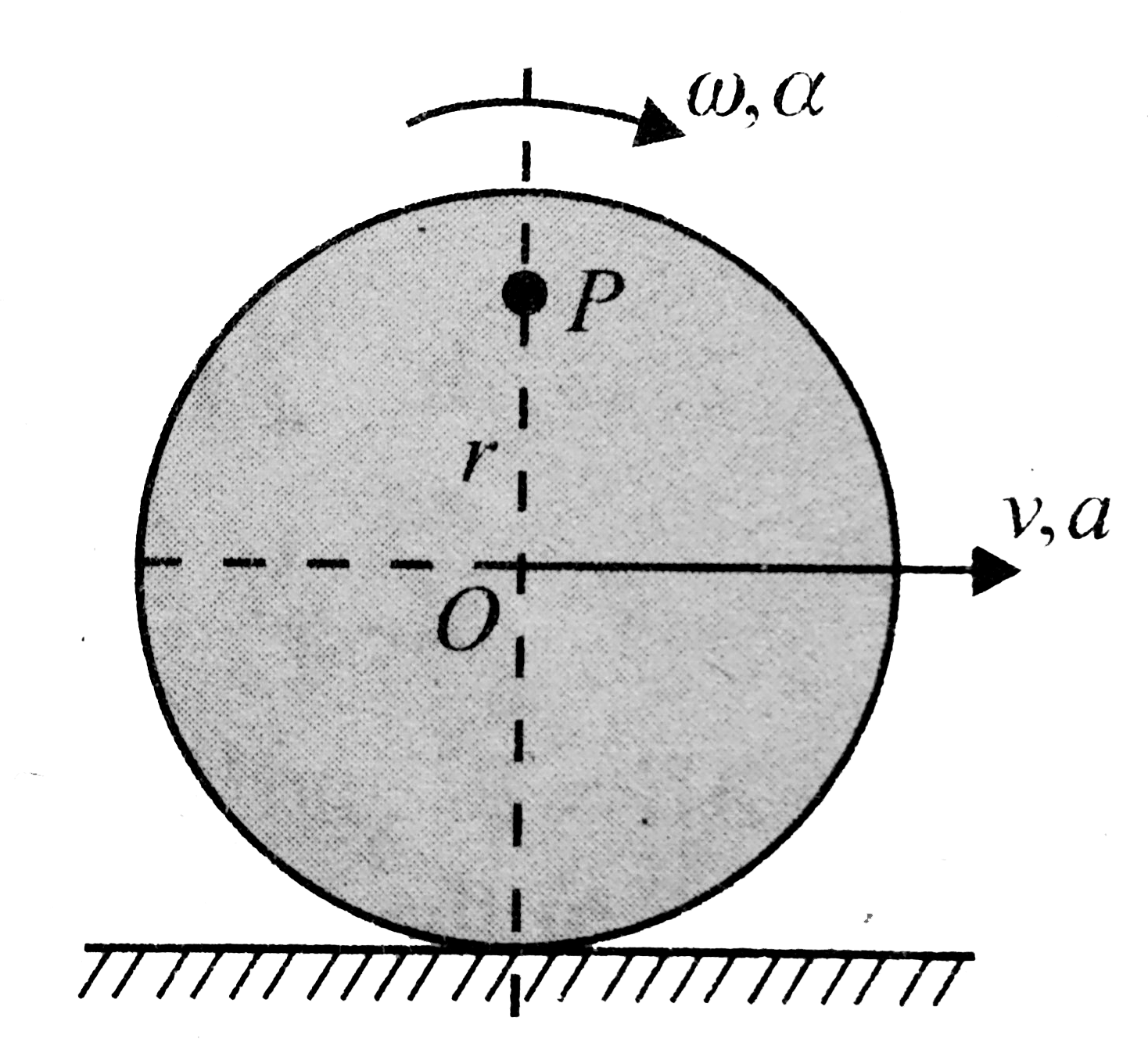
View SolutionA disc of radius R rolls on a horizontal ground with linear acceleration a and angular acceleration α as shown in Fig. The magnitude of acceleration of point P as shown in the figure at an instant when its linear velocity is v and angular velocity is ω will be a
View SolutionAssertion: Vector product of two vectors is an axial vector.
Reason: If →v= instantaneous Velocity, →r= radius vector and →ω= angular velocity, then →ω=→v×→r.
View SolutionThe linear velocity of a particle on a rotating body is given by →v=→ω×→r where →ω is the angular velocity and →r is the radius vector. What is the value of |v| if →ω=ˆi−2ˆj+2ˆkand→r=4ˆj−3ˆk ?
View Solution

