Assertion: If →A.→B=→B.→C, then →A may not always be equal to →C.
Reason: The dot product of two vectors involves consine of the angle between the two vectors.
If both assertion and reason are true and the reason is the correct explanation of the assertion.
If both assertion and reason are true but reason is not the correct explanation of the assertion
If assertion is true but reason is false.
If the assertion and reason both are false.
The correct Answer is:A
→A.→B=→B.→C
⇒ABcosθ1=BCcosθ2
When θ1=θ2then A= C
Topper's Solved these Questions
Similar Questions
Knowledge Check
If →a.→b=∣∣→a×→b∣∣, then angle between vector →a and vector →b is :
Aπ2Bπ6Cπ4Dπ3Assertion: If ∣∣→A+→B∣∣=∣∣→A−→B∣∣, then angle between →A and →B is 90∘
Reason: →A+→B=→B+→AAIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is false.DIf both aseertion and reason are false.Let →a and →b be two unit vectors and θ is the angle between them. Then →a+→b is a unit vector if :
Aθ=π4Bθ=π3Cθ=π2Dθ=2π3
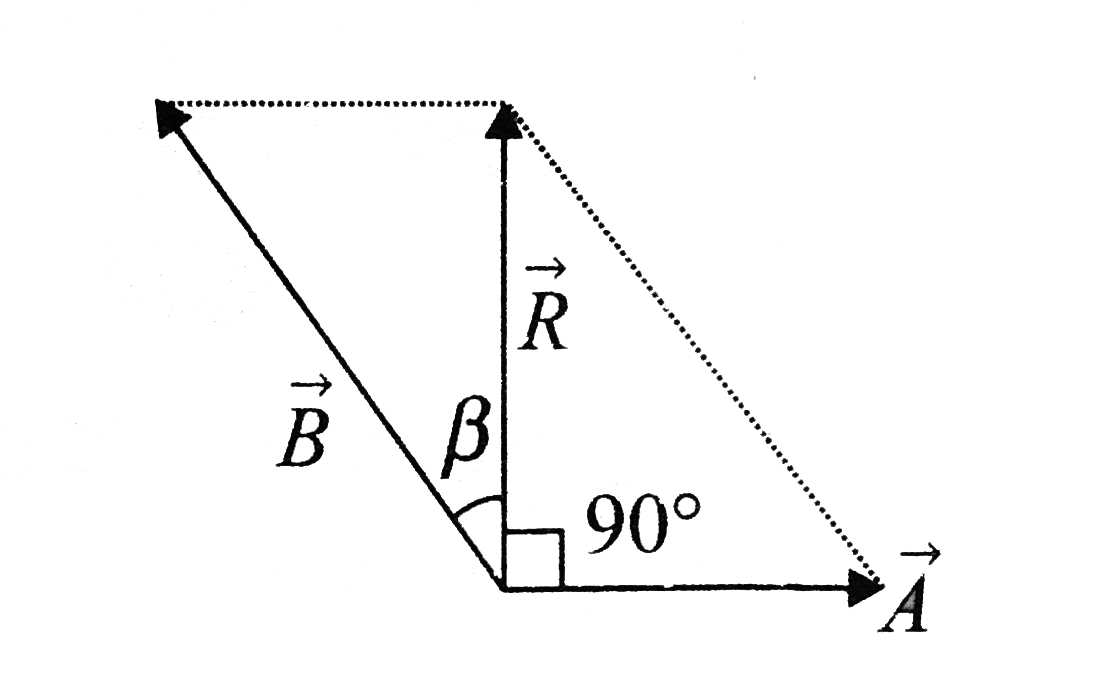
The resultant of two vectors →Aand→B perpendicular to the vector →Aanditsmagnitudequal→halfofthemagnitudeofthe→−−→r vec B.F∈doutthe∠between vec A and vec B.
View SolutionIf →aand→b are two non-zero vectors such that ∣∣→a×→b∣∣=→a.→b, then angle between →a and →b
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
View Solution→Aand→B are the two vectors such that ratio their dot product to magnitude of their cross product is 1√3. Then the angle between →Aand→B is
View SolutionFor any two vectors A and B, if →A.→B=∣∣→A×→B∣∣, the magnitude of →C=→A+→B is equal to :
View Solution
