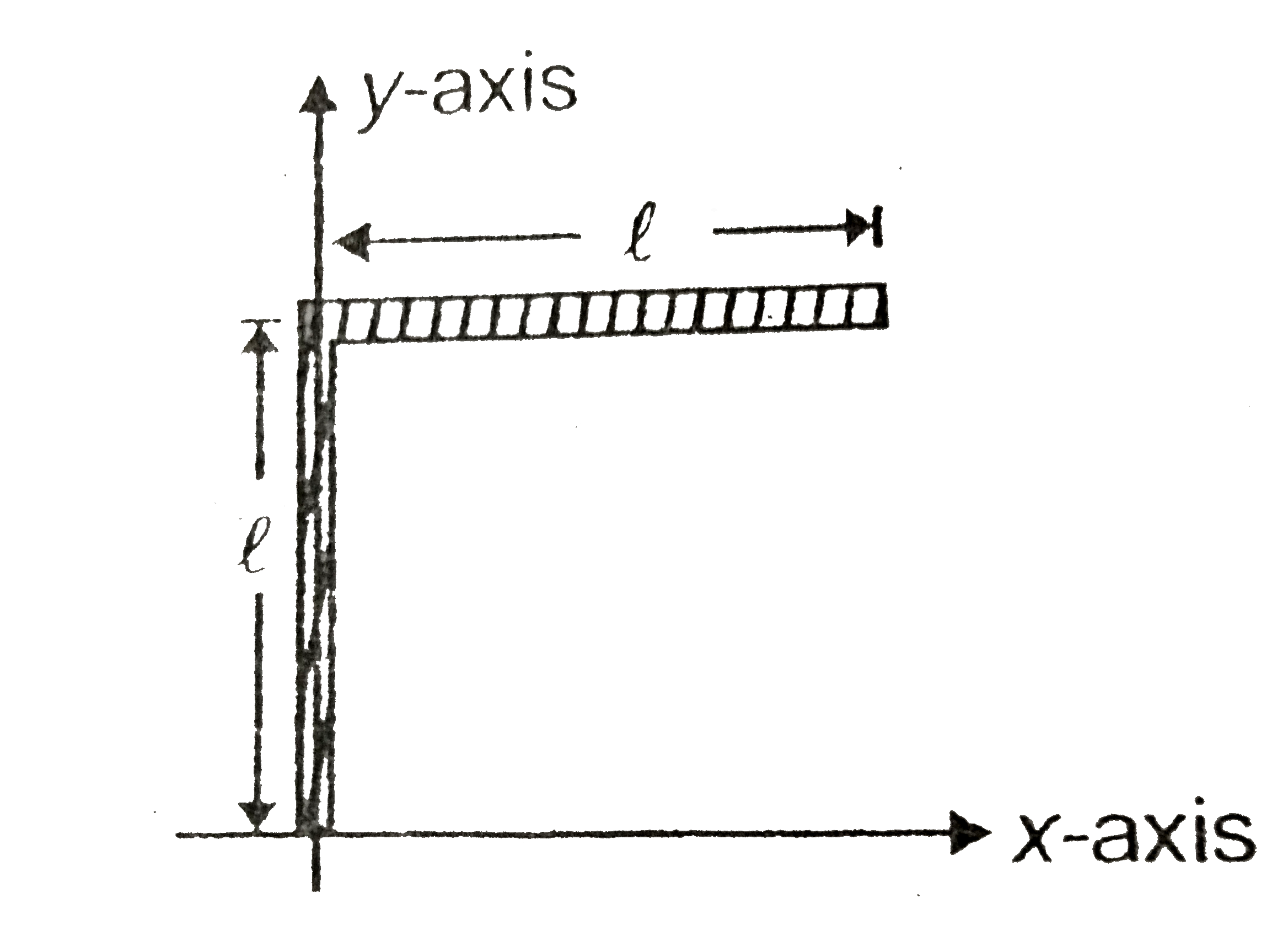Letter F is formed from three identical rods of length l. Find coordinates of its centre of mass.
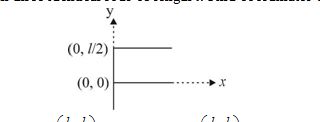
(l5,l5)
(l3,l6)
(l6,l3)
(l2,l5)
The correct Answer is:B
Step by step video, text & image solution for Letter F is formed from three identical rods of length l. Find coordinates of its centre of mass. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
A uniform wire is bent into the form of a rectangle of length L and width W. The coordinates of its centre of mass from a corner are
A(0,0)B(L2,W)C(L,W2)D(L2,W2)A rigid body is made of three identical thin rods, each of length L fastened together in the form of the letter H. The moment of inertia of this body about an axis that runs along the length of one of the legs of H is
AML23B4ML23CML2D3ML2You are supplied with three identical rods of same length and mass. If the length of each rod is 2π. Two of them are converted into rings and then placed over the third rod as shown in figure. If point A is considered as origin of the coordinate system the coordinate of the center of mass will be (you may assume AB as x-axis of the coordinate system).
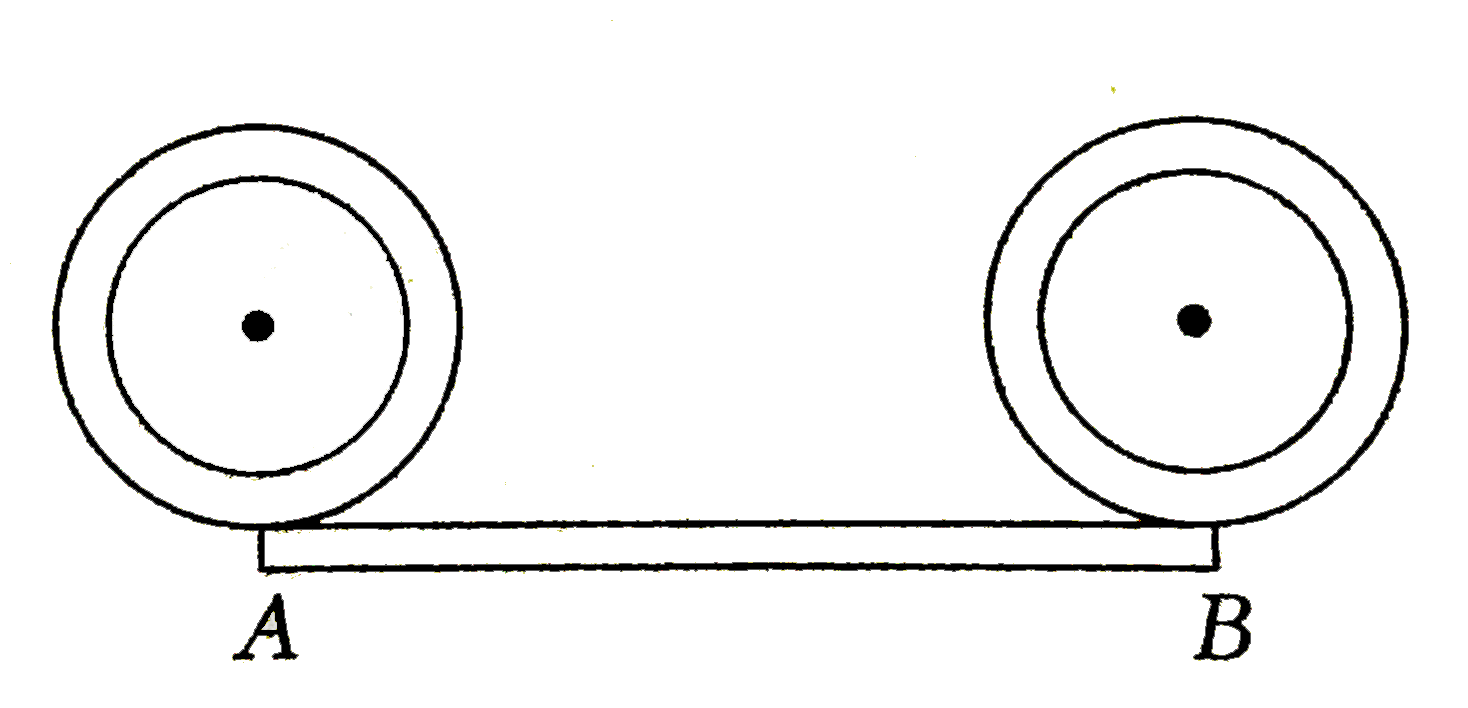 A(π2,13)B(π2,23)C(π,13)D(π,23)
A(π2,13)B(π2,23)C(π,13)D(π,23)
The moment of inertia of a rod of length l about an axis passing through its centre of mass and perpendicular to rod is I. The moment of inertia of hexagonal shape formed by six such rods, about an axis passing through its centre of mass and perpendicular to its plane will be
View SolutionThree rods of the same mass are placed as shown in the figure. Calculate the coordinates of the centre of mass of the system.
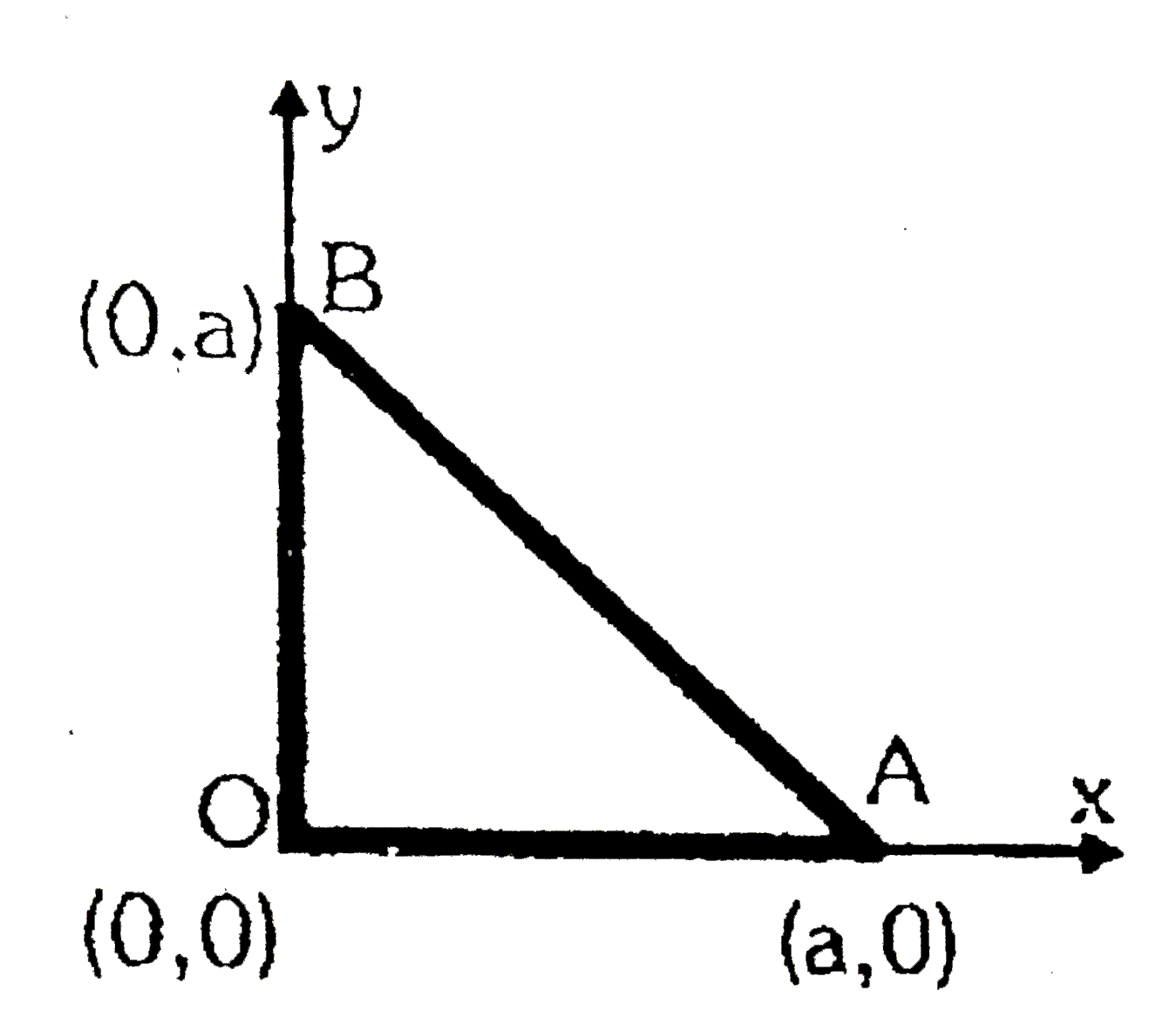
View SolutionA rod of mass m and length l is held vertically on a smooth horizontal floor. Now it is released from this position, find the speed of its centre of mass when it makes an angle θ with the vertical.
View SolutionInfinite rods of uniform mass density and length L,L/2,L/4….. Are placed one upon another upto infinite as shown in figure. Find the x-coordinate of centre of mass.

View SolutionThe moment of inertia of a rod of length l about an axis passing through its centre of mass and perpendicular to rod is I. The moment of inertia of hexagonal shape formed by six such rods, about an axis passing through its centre of mass and perpendicular to its plane will be
View Solution