A ball rolls down an inclined track 2 m long in 4s. Find
Speed of the ball at the bottom of track.
To find the speed of the ball at the bottom of the inclined track, we can follow these steps:
Step 1: Identify the known values
- Distance traveled (s) = 2 meters
- Time taken (t) = 4 seconds
- Initial velocity (u) = 0 m/s (since the ball starts from rest)
Step 2: Use the equation of motion to find acceleration
We can use the equation of motion:
s=ut+12at2
Substituting the known values:
2=0⋅4+12a(42)
2=12a⋅16
2=8a
Now, solve for acceleration (a):
a=28=14 m/s2
Step 3: Use the acceleration to find the final velocity
Now we can use another equation of motion to find the final velocity (v):
v=u+at
Substituting the known values:
v=0+(14)⋅4
v=1 m/s
Conclusion
The speed of the ball at the bottom of the track is 1 m/s.
---
- Distance traveled (s) = 2 meters
- Time taken (t) = 4 seconds
- Initial velocity (u) = 0 m/s (since the ball starts from rest)
We can use the equation of motion:
s=ut+12at2
2=0⋅4+12a(42)
2=12a⋅16
2=8a
a=28=14 m/s2
Now we can use another equation of motion to find the final velocity (v):
v=u+at
v=0+(14)⋅4
v=1 m/s
The speed of the ball at the bottom of the track is 1 m/s.
Topper's Solved these Questions
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERES
43 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - VERY SHORT ANSWER QUESTIONS
60 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems
30 Videos
Similar Questions
A ball rolls down an inclined plane and acquires a velocity vr when it reaches the bottom of the plane. If the same ball slides without friction and acquires rolling from the same height down an equally inclined smooth plane and acquires a velocity vs (then which of the following statements are not correct?
View SolutionA block of mass 1kg slides down a curved track which forms one quadrant of a circle of radius 1m as shown in figure. The speed of block at the bottom of track is v=2ms−1. The work done by the of friction is
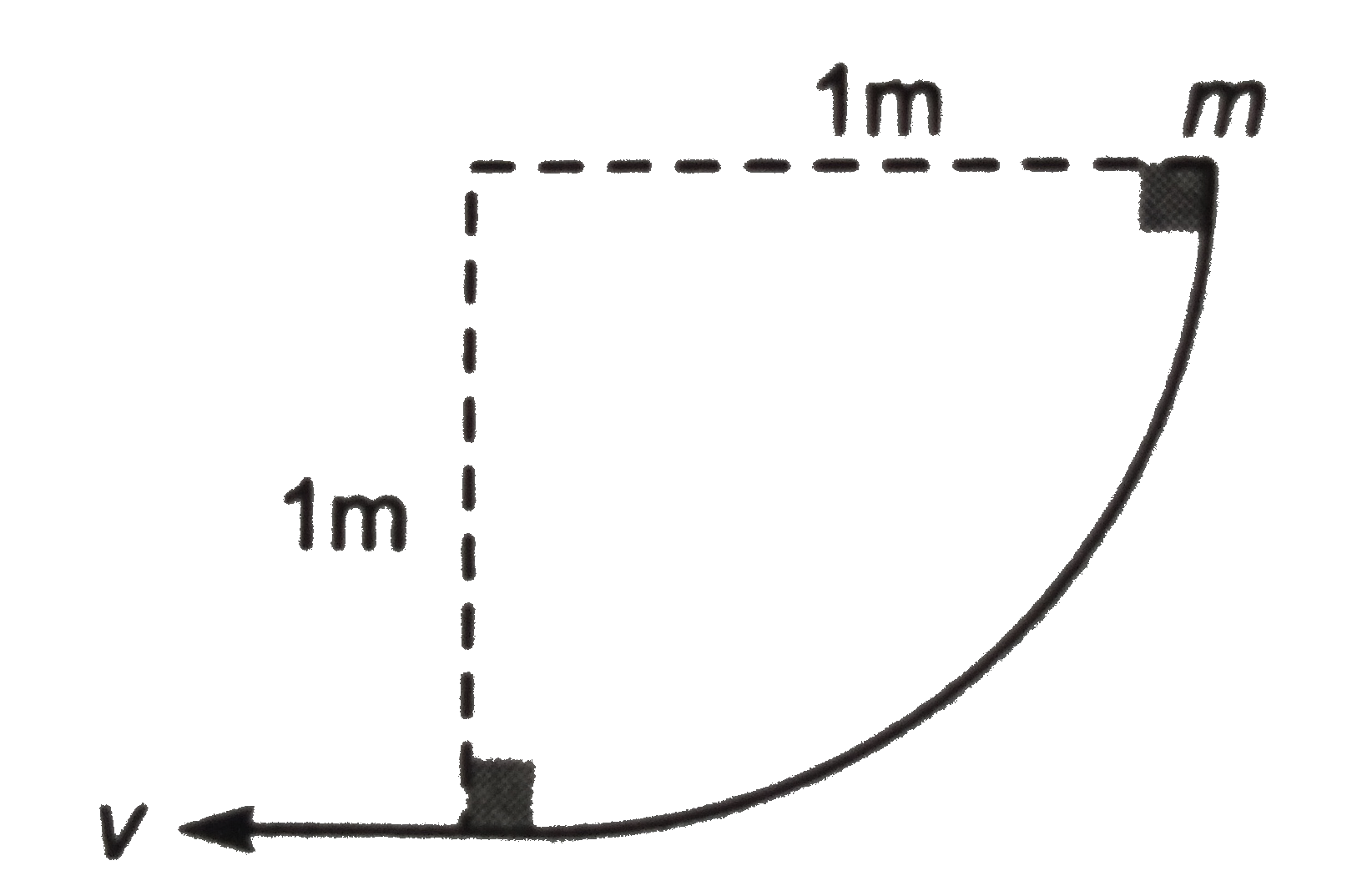 .
.
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rolls down an inclined plane without slipping. THE speed of its centre of mass when it reaches the bottom is
A√(2gh)B√4/3.ghC√3/4.ghD√(4g/h)
A solid cylinder rolls down an inclined plane of height 3m and reaches the bottom of plane with angular velocity of 2√2rad/s. The radius of cylinder must be [take g=10m/s2]
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View SolutionA solid cylinder of radius r rolls down an inclined plane of height h and inclination θ. Calculate its speed at the bottom of the plane using energy method. Also calculate the time taken to reach of the bottom.
View SolutionA uniform ring rolls down an inclined plane without slipping. If it reaches the bottom of a speed of 2m/s, then calculate the height of the inclined plane (use g=10m/s2)
View SolutionA uniform ring rolls down an inclined plane without slipping. If it reaches the bottom of a speed of 2m/s, then calculate the height of the inclined plane (use g=10m/s2)
View SolutionA solid cylinder 30 cm in diameter at the top of an inclined plane 2.0 m high is released and rolls down the incline without loss of energy due to friction. Its linear speed at the bottom is
View SolutionA ball is projected vertically up wards with a velocity of 100 m/s. Find the speed of the ball at half the maximum height. (g=10m/s2)
View Solution
