ABC is an isosceles triangle, right-angled at B. Similar trianles ACD and ABE are constructed on sides AC and AB. Find ratio between the areas of $Δ A B C and Δ A C D$ .

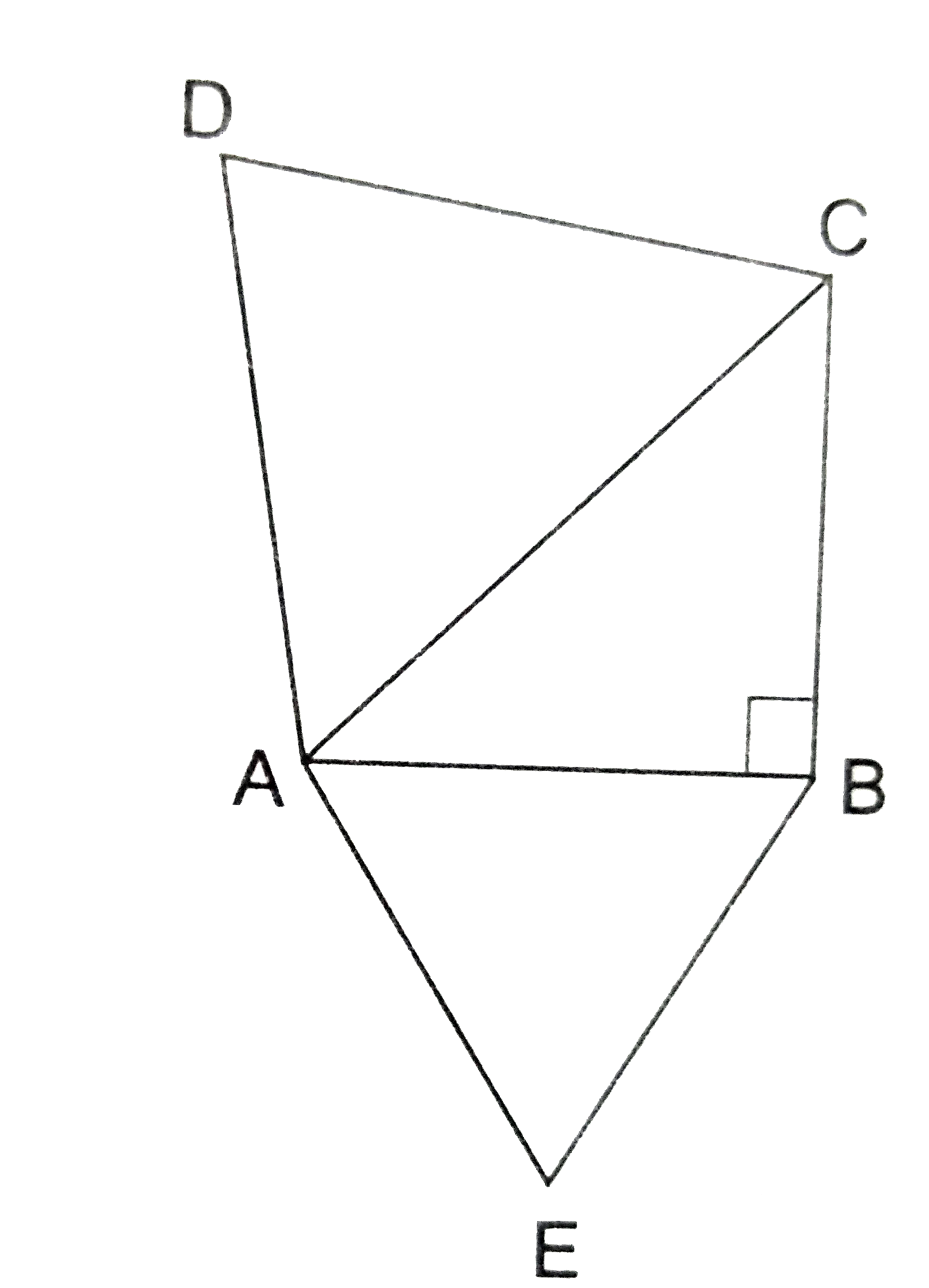
$3 : 2$

$2 : 3$

$\sqrt{2} : 1$

$1 : 2$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

Answer

Step by step video & text solution for ABC is an isosceles triangle, right-angled at B. Similar trianles ACD and ABE are constructed on sides AC and AB. Find ratio between the areas of Delta ABC and Delta ACD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

ABC is an isosceles triangle right angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. The ratio between the areas of $Δ A B E and Δ A C D$ is
A $\sqrt{2} : 1$
B $1 : 2$
C $2 : 1$
D $\sqrt{2} : 1$
ABC is an isosceles triangle, which is right angled at B with AB = 4 cm. What is the length of AC?
A2 cm
B2 $\sqrt{2}$ cm
C4 cm
D4 $\sqrt{2}$ cm

SCIENCE OLYMPIAD FOUNDATION -IMO QUESTION PAPER 2018 SET B-ACHIEVERS SECTION

Home
Ask Doubt
Profile

ABC is an isosceles triangle, right-angled at B. Similar trianles ACD and ABE are constructed on sides AC and AB. Find ratio between the areas of ΔABCandΔACD.

The correct Answer is:D

Topper's Solved these Questions

Similar Questions

Knowledge Check

ABC is an isosceles triangle right angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. The ratio between the areas of ΔABEandΔACD is

ABC is an isosceles triangle, which is right angled at B with AB = 4 cm. What is the length of AC?

SCIENCE OLYMPIAD FOUNDATION -IMO QUESTION PAPER 2018 SET B-ACHIEVERS SECTION

ABC is an isosceles triangle, right-angled at B. Similar trianles ACD and ABE are constructed on sides AC and AB. Find ratio between the areas of $Δ A B C and Δ A C D$ .

ABC is an isosceles triangle right angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. The ratio between the areas of $Δ A B E and Δ A C D$ is