AB is a line segment and M is its mid point. Semi-circles are drawn with AM, MB and AB as diameters on the same side of AB. A circle is drawn to touch all the three semi-circles. Its radius is :
AB3
23AB
AB6
34AB
The correct Answer is:C
To find the radius of the circle that touches all three semi-circles drawn on the line segment AB, we can follow these steps:
1. Define the Length of AB:
Let the length of line segment AB be AB=4x. Since M is the midpoint of AB, we have:
AM=MB=2x
2. Identify the Radii of the Semi-Circles:
- The radius of the semi-circle with diameter AM is:
r1=AM2=2x2=x
- The radius of the semi-circle with diameter MB is:
r2=MB2=2x2=x
- The radius of the semi-circle with diameter AB is:
r3=AB2=4x2=2x
3. Set Up the Geometry:
Let the radius of the circle that touches all three semi-circles be r. The center of this circle will be at a distance (2x−r) from point M (the midpoint of AB) and at a distance r from the other two semi-circles.
4. Use the Right Triangle Relationship:
We can form a right triangle with:
- One leg as the distance from the center of the circle to M, which is 2x−r.
- The other leg as the distance from the center of the circle to the point where it touches the semi-circle with diameter AB, which is r.
- The hypotenuse is the distance from the center of the circle to the center of the semi-circle with diameter AB, which is 2x.
Using the Pythagorean theorem:
(2x−r)2+r2=(2x)2
5. Expand and Simplify the Equation:
Expanding the left side:
(2x−r)2=4x2−4xr+r2
Thus, the equation becomes:
4x2−4xr+r2+r2=4x2
Simplifying gives:
2r2−4xr=0
6. Factor the Equation:
Factoring out 2r:
2r(r−2x)=0
This gives us two solutions:
r=0orr=2x
7. Find the Radius in Terms of AB:
Since r cannot be zero, we take r=2x. Recall that AB=4x, thus:
r=AB2
8. Final Result:
The radius of the circle that touches all three semi-circles is:
r=AB6
Let the length of line segment AB be AB=4x. Since M is the midpoint of AB, we have:
AM=MB=2x
- The radius of the semi-circle with diameter AM is:
r1=AM2=2x2=x
- The radius of the semi-circle with diameter MB is:
r2=MB2=2x2=x
- The radius of the semi-circle with diameter AB is:
r3=AB2=4x2=2x
Let the radius of the circle that touches all three semi-circles be r. The center of this circle will be at a distance (2x−r) from point M (the midpoint of AB) and at a distance r from the other two semi-circles.
We can form a right triangle with:
- One leg as the distance from the center of the circle to M, which is 2x−r.
- The other leg as the distance from the center of the circle to the point where it touches the semi-circle with diameter AB, which is r.
- The hypotenuse is the distance from the center of the circle to the center of the semi-circle with diameter AB, which is 2x.
(2x−r)2+r2=(2x)2
Expanding the left side:
(2x−r)2=4x2−4xr+r2
Thus, the equation becomes:
4x2−4xr+r2+r2=4x2
Simplifying gives:
2r2−4xr=0
Factoring out 2r:
2r(r−2x)=0
This gives us two solutions:
r=0orr=2x
Since r cannot be zero, we take r=2x. Recall that AB=4x, thus:
r=AB2
The radius of the circle that touches all three semi-circles is:
r=AB6
Similar Questions
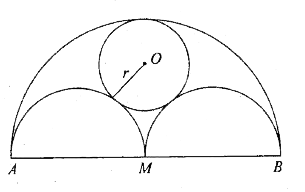
AB is a line segment of length 2a with M as mid-point. Semicircles are drawn on one side with AM, MB and AB as diameter as shown in the above figure. A circle .with centre O and radius r is drawn such that this circle touches all the three semicircles. The value of r is
View SolutionPQ is a lines segment and R is its midpoint. Semicircles are drawn at the same side of PQ taking PR,RQandPQ as diameters. A circle of radius r and centre O is drawn touching all the three semi circles.
Prove that r=16PQ
View Solution
Knowledge Check
AB is a line segment of length 48 cm and C is its mid-point. If three semicircles are drawn at AB, AC and CB using as diameters, then radius of the circle inscribed in the space enclosed by three semicircles is
A3√2B6C8D10In the given figure, M is the mid point of line segment AB whose length is 2a. Semicircles having diameters AM, MB and AB are drawn at the same side of the line. The radius of a circle toughing all the three semicircle is
 A2a3Ba2Ca3Da4
A2a3Ba2Ca3Da4PQ is a lines segment of 12 cm whose midpoint is R. Taking PR, RQ and PQ as diameters semicircles are drawn at the same side of PQ. The area of the circle that touches all the three circles is
A2πsq. cmB4π sq. cmC6π sq. cmD94 sq. cm
In Figure AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.
View SolutionIn the figure semicircles are drawn with PQ, PB and BQ as diameter. PB=BQ=21cm. A circle with centre O is drawn to touch all the three semicircles. Find its radius and also find the shaded region.

View SolutionTwo circles are drawn with sides AB and AC of a triangle ABC as diameters
View SolutionO is the mid-point of line segment AB of length 36cm. If the semicircles are drawn on AB, OA and OB as diameters, then the radius of the smallest circle which touches all the semicircles is(1) 6 cm (2) 9 cm (3) 12 cm (4) 4 cm.
View SolutionIn the given figure, AB is a line of length 2a and mid Point M. Taking AM, MB and AB as diameters semi circles are drawn on the same sides of the line. Taking centre O and radius 'r' a circle is drawn such that it touches all the three circles. Then find the value of r.
View Solution
