AB is a line segment of length 48 cm and C is its mid-point. If three semicircles are drawn at AB, AC and CB using as diameters, then radius of the circle inscribed in the space enclosed by three semicircles is
3√2
6
8
10
The correct Answer is:C
To find the radius of the circle inscribed in the space enclosed by three semicircles drawn on the line segment AB (length 48 cm) and its midpoints, we can follow these steps:
Step 1: Identify the lengths
- The length of line segment AB is given as 48 cm.
- The midpoint C divides AB into two equal segments: AC and CB, each measuring 24 cm.
Step 2: Draw semicircles
- Draw three semicircles:
1. The first semicircle has diameter AB (48 cm), so its radius is RAB=482=24 cm.
2. The second semicircle has diameter AC (24 cm), so its radius is RAC=242=12 cm.
3. The third semicircle has diameter CB (24 cm), so its radius is RCB=242=12 cm.
Step 3: Set up the triangle
- Consider triangle OXC, where O is the center of the semicircle on AB, X is the point where the inscribed circle touches AC, and C is the midpoint of AB.
- The lengths are:
- OC = 24 cm (radius of the semicircle on AB)
- XC = 12 cm (radius of the semicircle on AC)
- Let the radius of the inscribed circle be r.
Step 4: Apply the Pythagorean theorem
- In triangle OXC, by the Pythagorean theorem:
OX2=OC2−XC2
Substituting the known values:
(12+r)2=122+(24−r)2
Step 5: Expand and simplify
- Expanding both sides:
(12+r)2=144+(576−48r+r2)
144+24r+r2=720−48r+r2
Step 6: Cancel r2 and rearrange
- Cancel r2 from both sides:
144+24r=720−48r
- Rearranging gives:
24r+48r=720−144
72r=576
Step 7: Solve for r
- Dividing both sides by 72:
r=57672=8
Conclusion
The radius of the circle inscribed in the space enclosed by the three semicircles is r=8 cm.
- The length of line segment AB is given as 48 cm.
- The midpoint C divides AB into two equal segments: AC and CB, each measuring 24 cm.
- Draw three semicircles:
1. The first semicircle has diameter AB (48 cm), so its radius is RAB=482=24 cm.
2. The second semicircle has diameter AC (24 cm), so its radius is RAC=242=12 cm.
3. The third semicircle has diameter CB (24 cm), so its radius is RCB=242=12 cm.
- Consider triangle OXC, where O is the center of the semicircle on AB, X is the point where the inscribed circle touches AC, and C is the midpoint of AB.
- The lengths are:
- OC = 24 cm (radius of the semicircle on AB)
- XC = 12 cm (radius of the semicircle on AC)
- Let the radius of the inscribed circle be r.
- In triangle OXC, by the Pythagorean theorem:
OX2=OC2−XC2
Substituting the known values:
(12+r)2=122+(24−r)2
- Expanding both sides:
(12+r)2=144+(576−48r+r2)
144+24r+r2=720−48r+r2
- Cancel r2 from both sides:
144+24r=720−48r
- Rearranging gives:
24r+48r=720−144
72r=576
- Dividing both sides by 72:
r=57672=8
The radius of the circle inscribed in the space enclosed by the three semicircles is r=8 cm.
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type
9 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
7 Videos
- COMPLEX NUMBERSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - MATRIX MATCH TYPE
9 Videos
Similar Questions
AB is a line segment and M is its mid point. Three semi circles are drawn with AM, MB and AB as diameters on the same side of the line AB. A circle with radius r unit is drawn so that it touches all thethree semi- circles. Show that AB=6×r
View SolutionIn Figure AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.
View SolutionDraw a line segment AB of length 5 cm using a ruler.
View SolutionAB is the diameter of a semicircle k,C is an arbitrary point on the semicircle (other than A or B) and S is the centre of the circle inscribed into triangle ABC, then measure of-
View SolutionDraw a line segment AB of length 5 cm using ruler and compass
View SolutionIn the given figure ΔABC is right angled at A. Semicircles are drawn on AB, BC and AC as diameters. It is given that AB=3 cm and AC=4cm then find the area of the shaded region
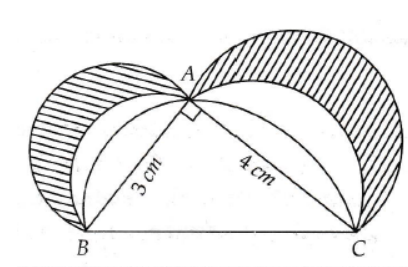
View SolutionDraw a line segment AB of length 5.3 cm. using two different methods bisect AB.
View SolutionIn a right -angle triangle, the length of the sides containing the right angles are aandb. With the mid-point of each sides as centres three semicircles are drawn outiside the triangle. Find the area of Δ and the semicircles together
View SolutionABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their cintres. Find the radius of the three circles.
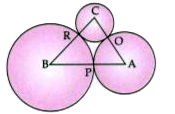
View SolutionABC is a triangle with AB=10cm, BC=8cm and AC=6cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres Find the radii of the three circles.
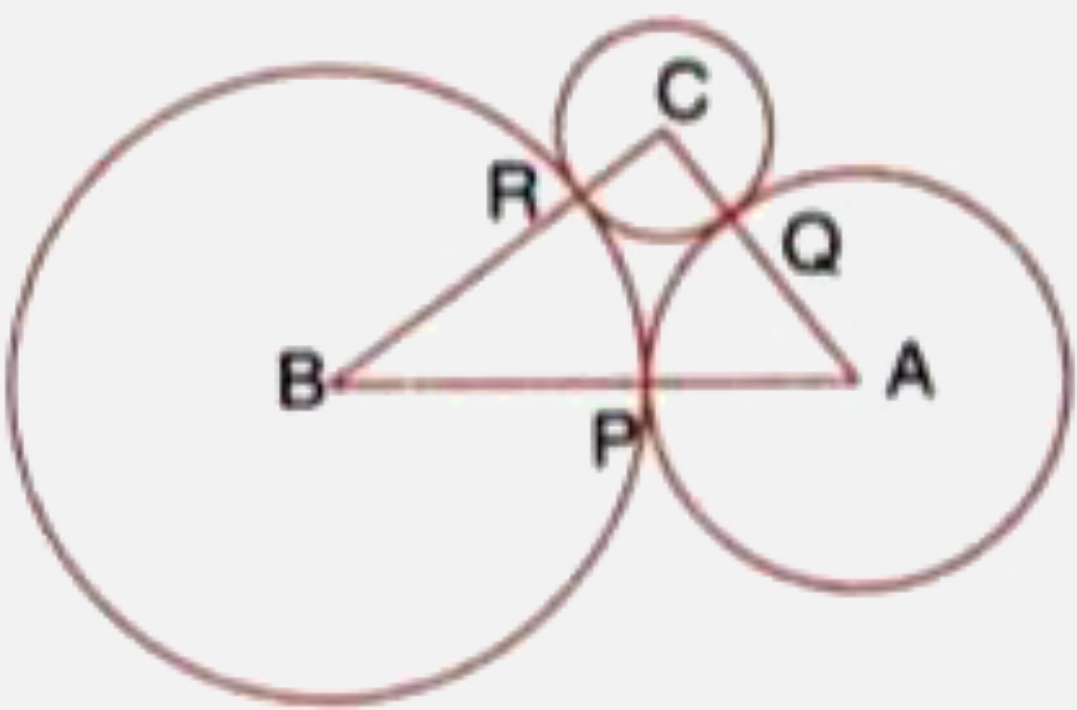
View Solution
